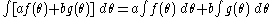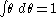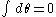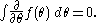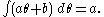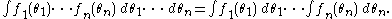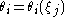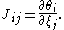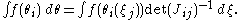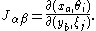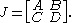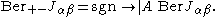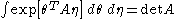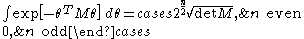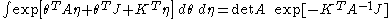Berezin integral
Encyclopedia
In mathematical physics
, a Grassmann
integral, or, more correctly, Berezin integral
, is a way to define integration for functions of Grassmann variables. It is not an integral
in the Lebesgue sense; it is called integration because it has analogous properties and since it is used in physics as a sum over histories for fermion
s, an extension of the path integral
. The technique was invented by the Russian mathematician Felix Berezin
and developed in his textbook. Some earlier insights were made by the physicist David John Candlin
in 1956.
where we define
so that :
These properties define the integral uniquely.
This is the most general function, because every homogeneous function of one Grassmann variable is either constant or linear.
Note that the sign of the result depends on the order of integration.
Suppose now we want to do a substitution:
where as usual (ξj) implies dependence on all ξj. Moreover the function θi has to be an odd function, i.e. contains an odd number of ξj in each summand. The Jacobian is the usual matrix
the substitution formula now reads as
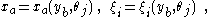where xa are even functions and θi are odd functions. We assume the functions xa and θi to be defined on an open set U in Rm. The functions xa map onto the open set U' in Rm.
The change of the integral will depend on the Jacobian
This matrix consists of four blocks:
A and D are even functions due to the derivation properties, B and C are odd functions. A matrix of this block structure is called even matrix.
The transformation factor itself depends on the oriented Berezinian
of the Jacobian. This is defined as:
For further details see the article about the Berezinian.
The complete formula now reads as:
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, a Grassmann
Hermann Grassmann
Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...
integral, or, more correctly, Berezin integral
Berezin integral
In mathematical physics, a Grassmann integral, or, more correctly, Berezin integral, is a way to define integration for functions of Grassmann variables. It is not an integral in the Lebesgue sense; it is called integration because it has analogous properties and since it is used in physics as a...
, is a way to define integration for functions of Grassmann variables. It is not an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
in the Lebesgue sense; it is called integration because it has analogous properties and since it is used in physics as a sum over histories for fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s, an extension of the path integral
Path integral
Path integral may refer to:* Line integral, the integral of a function along a curve* Functional integration, the integral of a functional over a space of curves...
. The technique was invented by the Russian mathematician Felix Berezin
Felix Berezin
Felix Alexandrovich Berezin was a Soviet Russian mathematician and physicist known for his contributions to the theory of supersymmetry and supermanifolds as well as to the path integral formulation of quantum field theory....
and developed in his textbook. Some earlier insights were made by the physicist David John Candlin
David John Candlin
David John Candlin was a British born physicist. He is known for developing the path integral formulation of the Fermionic field, inventing Grassmann integration for this purpose. Candlin was born in the town of Mitchum, in Surrey, England. He received his PhD in 1955, and wrote his influential...
in 1956.
Definition
The Berezin integral is defined to be a linear functional
where we define
so that :
These properties define the integral uniquely.
This is the most general function, because every homogeneous function of one Grassmann variable is either constant or linear.
Multiple variables
Integration over multiple variables is defined by Fubini's theorem:
Note that the sign of the result depends on the order of integration.
Suppose now we want to do a substitution:
where as usual (ξj) implies dependence on all ξj. Moreover the function θi has to be an odd function, i.e. contains an odd number of ξj in each summand. The Jacobian is the usual matrix
the substitution formula now reads as
Substitution formula
Consider now a mixture of even and odd variables, i.e. xa and θi. Again we assume a coordinate transformation as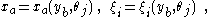 where xa are even functions and θi are odd functions. We assume the functions xa and θi to be defined on an open set U in Rm. The functions xa map onto the open set U' in Rm.The change of the integral will depend on the Jacobian
This matrix consists of four blocks:
A and D are even functions due to the derivation properties, B and C are odd functions. A matrix of this block structure is called even matrix.
The transformation factor itself depends on the oriented Berezinian
Berezinian
In mathematics and theoretical physics, the Berezinian or superdeterminant is a generalization of the determinant to the case of supermatrices. The name is for Felix Berezin...
of the Jacobian. This is defined as:
For further details see the article about the Berezinian.
The complete formula now reads as:
-
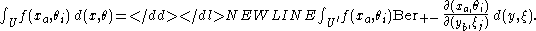
Gaussian integrals over Grassmann variables
The following formulas for Gaussian integrals are used often in the path integral formulationPath integral formulationThe path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
:
with
being a 
matrix.
with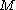
being an 
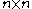antisymmetric matrix.
In the above formulas the notation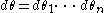
is used.
From the above formulas, other useful formulas follow:
with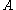
being an invertible 
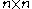matrix, 
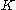and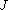 
are Grassmann variables.
with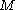
being an invertible 
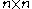antisymmetric matrix, and 
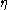Grassmann variable.
Literature
- Theodore Voronov: Geometric integration theory on Supermanifolds, Harwood Academic Publisher, ISBN 3-7186-5199-8
-
