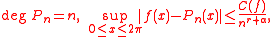Bernstein's theorem (approximation theory)
Encyclopedia
In approximation theory
, Bernstein's theorem is a converse to Jackson's theorem
. The first results of this type were proved by Sergei Bernstein in 1912.
For approximation by trigonometric polynomials, the result is as follows:
Let f: [0, 2π] → C be a 2π-periodic function
, and assume r is a natural number, and 0 < α < 1. If there exists a number C(f) > 0 and a sequence of trigonometric polynomial
s {Pn}n ≥ n0 such that
then f = Pn0 + φ, where φ has a bounded r-th derivative which is α-Hölder continuous
.
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
, Bernstein's theorem is a converse to Jackson's theorem
Jackson's inequality
In approximation theory, Jackson's inequality is an inequality bounding the value of function's best approximation by algebraic or trigonometric polynomials in terms of the modulus of continuity of its derivatives...
. The first results of this type were proved by Sergei Bernstein in 1912.
For approximation by trigonometric polynomials, the result is as follows:
Let f: [0, 2π] → C be a 2π-periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
, and assume r is a natural number, and 0 < α < 1. If there exists a number C(f) > 0 and a sequence of trigonometric polynomial
Trigonometric polynomial
In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin and cos with n a natural number. The coefficients may be taken as real numbers, for real-valued functions...
s {Pn}n ≥ n0 such that
then f = Pn0 + φ, where φ has a bounded r-th derivative which is α-Hölder continuous
Hölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
.