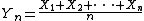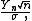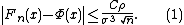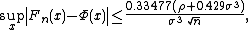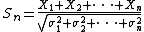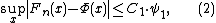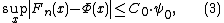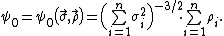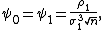The central limit theorem

Central limit theorem

In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...

 in probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

 and statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

 states that under certain circumstances the sample mean, considered as a random quantity, becomes more normally distributed as the sample size is increased. The Berry–Esseen theorem, also known as the Berry–Esseen inequality, attempts to quantify the rate at which this convergence to normality takes place.

Statement of the theorem

Statements of the theorem vary, as it was independently discovered by two mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

s, Andrew C. Berry (in 1941) and Carl-Gustav Esseen

Carl-Gustav Esseen

Carl-Gustav Esseen was a Swedish mathematician. His work was in the theory of probability. The Berry–Esseen theorem is named after him.-Life:...

 (1942), who then, along with other authors, refined it repeatedly over subsequent decades.

Identically distributed summands

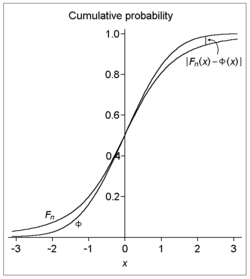
One version, sacrificing generality somewhat for the sake of clarity, is the following:

Let X₁, X₂, ..., be i.i.d. random variables with E

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

(X₁) = 0, E(X₁²) = σ² > 0, and E(|X₁|³) = ρ < ∞. Also, let

be the sample mean, with F_n the cdf

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

 of

and Φ the cdf of the standard normal distribution. Then there exists a positive constant

Constant (mathematics)

In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...

 C such that for all x and n,

That is: given a sequence of independent and identically-distributed random variables, each having mean

Mean

In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....

 zero and positive variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

, if additionally the third absolute moment

Moment (mathematics)

In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...

 is finite, then the cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

s of the standardized

Standard score

In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...

 sample mean and the standard normal distribution differ (vertically, on a graph) by no more than the specified amount. Note that the rate of convergence is on the order

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

 of n^−1/2.

Calculated values of the constant C have decreased markedly over the years, from the original value of 7.59 by , to 0.7882 by , then 0.7655 by , then 0.7056 by , then 0.7005 by , then 0.5894 by , then 0.5129 by , then 0.4785 by . The detailed review can be found in the papers , . The best estimate , C<0.4784, follows from the inequality

due to , since σ³≤ρ and 0.33477·1.429<0.4784.

proved that the bound must satisfy

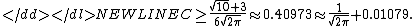
Non-identically distributed summands

Let X₁, X₂, ..., be independent random variables with E

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

(X_i) = 0, E(X_i²) = σ_i² > 0, and E(|X_i|³) = ρ_i < ∞. Also, let

be the normalized n-th partial sum. Denote F_n the cdf

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

 of S_n, and Φ the cdf of the standard normal distribution. For the sake of convenience denote

In 1941, Andrew C. Berry proved that for all n there exists an absolute constant C₁ such that

where

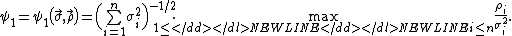
Independently, in 1942, Carl-Gustav Esseen

Carl-Gustav Esseen

Carl-Gustav Esseen was a Swedish mathematician. His work was in the theory of probability. The Berry–Esseen theorem is named after him.-Life:...

 proved that for all n there exists an absolute constant C₀ such that

where

It is easy to make sure that ψ₀≤ψ₁. Due to this circumstance inequality (3) is conventionally called the Berry-Esseen inequality, and the quantity ψ₀ is called the Lyapunov fraction of the third order. Moreover, in the case where the summands X₁,... X_n have identical distributions

and thus the bounds stated by inequalities (1), (2) and (3) coincide.

Regarding C₀, obviously, the lower bound established by remains valid:

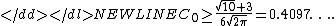
The upper bounds for C₀ were subsequently lowered from the original estimate 7.59 due to to (we mention the recent results only) 0.9051 due to , 0.7975 due to , 0.7915 due to , 0.6379 and 0.5606 due to and . the best estimate is 0.5600 obtained by .

See also

• Chernoff's inequality
• Edgeworth series
  Edgeworth series
  The Gram–Charlier A series , and the Edgeworth series are series that approximate a probability distribution in terms of its cumulants...
  
  
• List of inequalities
• List of mathematical theorems

External links

• Gut, Allan & Holst Lars. Carl-Gustav Esseen, retrieved Mar. 15, 2004.

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.