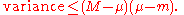In mathematics, the Bhatia–Davis inequality, named after Rajendra Bhatia and Chandler Davis, is an upper bound

Upper bound

In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...

 on the variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

 of any bounded probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

 on the real line.

Suppose a distribution has minimum m, maximum M, and expected value

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

 μ. Then the inequality says:

Equality holds precisely if all of the probability is concentrated at the endpoints m and M.

The Bhatia–Davis inequality is stronger than Popoviciu's inequality on variances

Popoviciu's inequality on variances

In probability theory, Popoviciu's inequality, named after Tiberiu Popoviciu, is an upper bound on the variance of any bounded probability distribution. Let M and m be upper and lower bounds on the values of any random variable with a particular probability distribution...

.