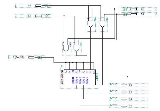
Binary multiplier
Encyclopedia
A binary multiplier is an electronic circuit
used in digital electronics, such as a computer
, to multiply
two binary numbers. It is built using binary adders.
A variety of computer arithmetic techniques can be used to implement a digital multiplier. Most techniques involve computing a set of partial products, and then summing the partial products together. This process is similar to the method taught to primary schoolchildren for conducting long multiplication on base-10 integers, but has been modified here for application to a base-2 (binary
) numeral system
.
which repeatedly shifts and accumulates partial results,
often written using loop unwinding
. Mainframe computer
s had multiply instructions, but they did the same sorts of shifts and adds as a "multiply routine".
Early microprocessor
s also had no multiply instruction. The Motorola 6809
, introduced in 1978, was one of the earliest microprocessors with a dedicated hardware multiply instruction.
It did the same sorts of shifts and adds as a "multiply routine", but implemented in the microcode
of the MUL instruction.
As more transistors per chip
became available due to larger-scale integration, it became possible to put enough adders on a single chip to sum all the partial products at once, rather than reuse a single adder to handle each partial product one at a time.
Because some common digital signal processing
algorithms spend most of their time multiplying, digital signal processor
designers sacrifice a lot of chip area in order to make the multiply as fast as possible; a single-cycle multiply–accumulate unit often used up most of the chip area of early DSPs.
123
x 456
56088
A binary computer does exactly the same, but with binary numbers. In binary encoding each long number is multiplied by one digit (either 0 or 1), and that is much easier than in decimal, as the product by 0 or 1 is just 0 or the same number. Therefore, the multiplication of two binary numbers comes down to calculating partial products (which are 0 or the first number), shifting them left, and then adding them together (a binary addition, of course):
1011 (this is 11 in binary)
x 1110 (this is 14 in binary)
10011010 (this is 154 in binary)
This is much simpler than in the decimal system, as there is no table of multiplication to remember: just shifts and adds.
This method is mathematically correct, but it has two serious engineering problems. The first is that it involves 32 intermediate additions in a 32-bit computer, or 64 intermediate additions in a 64-bit computer. These additions take a lot of time. The engineering implementation of binary multiplication consists, really, of taking a very simple mathematical process and complicating it a lot, in order to do fewer additions; a modern processor can multiply two 64-bit numbers with 16 additions (rather than 64), and can do several steps in parallel—but at a cost of making the process almost unreadable.
The second problem is that the basic school method handles the sign with a separate rule ("+ with + yields +", "+ with - yields -", etc.). Modern computers embed the sign of the number in the number itself, usually in the two's complement
representation. That forces the multiplication process to be adapted to handle two's complement numbers, and that complicates the process a bit more. Similarly, processors that use ones' complement, sign-and-magnitude, IEEE-754 or other binary representations require specific adjustments to the multiplication process.
eight bit integers together: a[7:0] and b[7:0]. We can produce eight partial products by performing eight one-bit multiplications, one for each bit in multiplicand a:
p0[7:0] = a[0] × b[7:0] = {8{a[0]}} & b[7:0]
p1[7:0] = a[1] × b[7:0] = {8{a[1]}} & b[7:0]
p2[7:0] = a[2] × b[7:0] = {8{a[2]}} & b[7:0]
p3[7:0] = a[3] × b[7:0] = {8{a[3]}} & b[7:0]
p4[7:0] = a[4] × b[7:0] = {8{a[4]}} & b[7:0]
p5[7:0] = a[5] × b[7:0] = {8{a[5]}} & b[7:0]
p6[7:0] = a[6] × b[7:0] = {8{a[6]}} & b[7:0]
p7[7:0] = a[7] × b[7:0] = {8{a[7]}} & b[7:0]
where{8{a[0]}} means repeating a[0] (the 0th bit of a) 8 times (Verilog notation).
To produce our product, we then need to add up all eight of our partial products, as shown here:
p0[7] p0[6] p0[5] p0[4] p0[3] p0[2] p0[1] p0[0]
+ p1[7] p1[6] p1[5] p1[4] p1[3] p1[2] p1[1] p1[0] 0
+ p2[7] p2[6] p2[5] p2[4] p2[3] p2[2] p2[1] p2[0] 0 0
+ p3[7] p3[6] p3[5] p3[4] p3[3] p3[2] p3[1] p3[0] 0 0 0
+ p4[7] p4[6] p4[5] p4[4] p4[3] p4[2] p4[1] p4[0] 0 0 0 0
+ p5[7] p5[6] p5[5] p5[4] p5[3] p5[2] p5[1] p5[0] 0 0 0 0 0
+ p6[7] p6[6] p6[5] p6[4] p6[3] p6[2] p6[1] p6[0] 0 0 0 0 0 0
+ p7[7] p7[6] p7[5] p7[4] p7[3] p7[2] p7[1] p7[0] 0 0 0 0 0 0 0
-------------------------------------------------------------------------------------------
P[15] P[14] P[13] P[12] P[11] P[10] P[9] P[8] P[7] P[6] P[5] P[4] P[3] P[2] P[1] P[0]
In other words, P[15:0] is produced by summing p0, p1 << 1, p2 << 2, and so forth, to produce our final unsigned 16-bit product.
integer instead of an unsigned
integer, then the partial products would need to have been sign-extended up to the width of the product before summing. If a had been a signed integer, then partial product p7 would need to be subtracted from the final sum, rather than added to it.
The above array multiplier can be modified to support two's complement notation signed numbers by inverting several of the product terms and inserting a one to the left of the first partial product term:
1 -p0[7] p0[6] p0[5] p0[4] p0[3] p0[2] p0[1] p0[0]
-p1[7] +p1[6] +p1[5] +p1[4] +p1[3] +p1[2] +p1[1] +p1[0] 0
-p2[7] +p2[6] +p2[5] +p2[4] +p2[3] +p2[2] +p2[1] +p2[0] 0 0
-p3[7] +p3[6] +p3[5] +p3[4] +p3[3] +p3[2] +p3[1] +p3[0] 0 0 0
-p4[7] +p4[6] +p4[5] +p4[4] +p4[3] +p4[2] +p4[1] +p4[0] 0 0 0 0
-p5[7] +p5[6] +p5[5] +p5[4] +p5[3] +p5[2] +p5[1] +p5[0] 0 0 0 0 0
-p6[7] +p6[6] +p6[5] +p6[4] +p6[3] +p6[2] +p6[1] +p6[0] 0 0 0 0 0 0
1 +p7[7] -p7[6] -p7[5] -p7[4] -p7[3] -p7[2] -p7[1] -p7[0] 0 0 0 0 0 0 0
------------------------------------------------------------------------------------------------------------
P[15] P[14] P[13] P[12] P[11] P[10] P[9] P[8] P[7] P[6] P[5] P[4] P[3] P[2] P[1] P[0]
Do not be misled by the minus sign (-) notation above. It does not mean arithmetic negation ( -(7) = -7), but instead binary complementation, more commonly denoted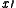
(read x prime), 
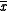(x bar) or ~
(tilde x), achieved by flipping all the bits. In two's complement to get the negation of a number, you complement the number then add 1, so they are NOT equivalent.
There are a lot of simplifications in the bit array above that are not shown and are not obvious. The sequences of one complemented bit followed by noncomplemented bits are implementing a two's complement trick to avoid sign extension. The sequence of p7 (noncomplemented bit followed by all complemented bits) is because we're subtracting this term so they were all negated to start out with (and a 1 was added in the least significant position). For both types of sequences, the last bit is flipped and an implicit -1 should be added directly below the MSB. When the +1 from the two's complement negation for p7 in bit position 0 (LSB) and all the -1's in bit columns 7 through 14 (where each of the MSBs are located) are added together, they can be simplified to the single 1 that "magically" is floating out to the left. For an explanation and proof of why flipping the MSB saves us the sign extension, see a computer arithmetic book .
s, or Dadda multiplier
s to add the partial products together in a single cycle. The performance of the Wallace tree
implementation is sometimes improved by modified Booth encoding one of the two multiplicands, which reduces the number of partial products that must be summed.
Electronic circuit
An electronic circuit is composed of individual electronic components, such as resistors, transistors, capacitors, inductors and diodes, connected by conductive wires or traces through which electric current can flow...
used in digital electronics, such as a computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
, to multiply
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
two binary numbers. It is built using binary adders.
A variety of computer arithmetic techniques can be used to implement a digital multiplier. Most techniques involve computing a set of partial products, and then summing the partial products together. This process is similar to the method taught to primary schoolchildren for conducting long multiplication on base-10 integers, but has been modified here for application to a base-2 (binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
) numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
.
History
Until the late 1970s, most minicomputers did not have a multiply instruction, and so programmers used a "multiply routine"which repeatedly shifts and accumulates partial results,
often written using loop unwinding
Loop unwinding
Loop unwinding, also known as loop unrolling, is a loop transformation technique that attempts to optimize a program's execution speed at the expense of its binary size...
. Mainframe computer
Mainframe computer
Mainframes are powerful computers used primarily by corporate and governmental organizations for critical applications, bulk data processing such as census, industry and consumer statistics, enterprise resource planning, and financial transaction processing.The term originally referred to the...
s had multiply instructions, but they did the same sorts of shifts and adds as a "multiply routine".
Early microprocessor
Microprocessor
A microprocessor incorporates the functions of a computer's central processing unit on a single integrated circuit, or at most a few integrated circuits. It is a multipurpose, programmable device that accepts digital data as input, processes it according to instructions stored in its memory, and...
s also had no multiply instruction. The Motorola 6809
Motorola 6809
The Motorola 6809 is an 8-bit microprocessor CPU from Motorola, designed by Terry Ritter and Joel Boney and introduced 1978...
, introduced in 1978, was one of the earliest microprocessors with a dedicated hardware multiply instruction.
It did the same sorts of shifts and adds as a "multiply routine", but implemented in the microcode
Microcode
Microcode is a layer of hardware-level instructions and/or data structures involved in the implementation of higher level machine code instructions in many computers and other processors; it resides in special high-speed memory and translates machine instructions into sequences of detailed...
of the MUL instruction.
As more transistors per chip
Transistor count
The transistor count of a device is the number of transistors in the device.Transistor count is the most common measure of integrated circuit complexity. According to Moore's Law, the transistor count of the integrated circuits doubles every two years...
became available due to larger-scale integration, it became possible to put enough adders on a single chip to sum all the partial products at once, rather than reuse a single adder to handle each partial product one at a time.
Because some common digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
algorithms spend most of their time multiplying, digital signal processor
Digital signal processor
A digital signal processor is a specialized microprocessor with an architecture optimized for the fast operational needs of digital signal processing.-Typical characteristics:...
designers sacrifice a lot of chip area in order to make the multiply as fast as possible; a single-cycle multiply–accumulate unit often used up most of the chip area of early DSPs.
Multiplication basics
The method taught in school for multiplying decimal numbers is based on calculating partial products, shifting them to the left and then adding them together. The most difficult part is to obtain the partial products, as that involves multiplying a long number by one digit (from 0 to 9):x 456
738 (this is 123 x 6)
615 (this is 123 x 5, shifted one position to the left)
+ 492 (this is 123 x 4, shifted two positions to the left)
56088
A binary computer does exactly the same, but with binary numbers. In binary encoding each long number is multiplied by one digit (either 0 or 1), and that is much easier than in decimal, as the product by 0 or 1 is just 0 or the same number. Therefore, the multiplication of two binary numbers comes down to calculating partial products (which are 0 or the first number), shifting them left, and then adding them together (a binary addition, of course):
1011 (this is 11 in binary)
x 1110 (this is 14 in binary)
0000 (this is 1011 x 0)
1011 (this is 1011 x 1, shifted one position to the left)
1011 (this is 1011 x 1, shifted two positions to the left)
+ 1011 (this is 1011 x 1, shifted three positions to the left)
10011010 (this is 154 in binary)
This is much simpler than in the decimal system, as there is no table of multiplication to remember: just shifts and adds.
This method is mathematically correct, but it has two serious engineering problems. The first is that it involves 32 intermediate additions in a 32-bit computer, or 64 intermediate additions in a 64-bit computer. These additions take a lot of time. The engineering implementation of binary multiplication consists, really, of taking a very simple mathematical process and complicating it a lot, in order to do fewer additions; a modern processor can multiply two 64-bit numbers with 16 additions (rather than 64), and can do several steps in parallel—but at a cost of making the process almost unreadable.
The second problem is that the basic school method handles the sign with a separate rule ("+ with + yields +", "+ with - yields -", etc.). Modern computers embed the sign of the number in the number itself, usually in the two's complement
Two's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
representation. That forces the multiplication process to be adapted to handle two's complement numbers, and that complicates the process a bit more. Similarly, processors that use ones' complement, sign-and-magnitude, IEEE-754 or other binary representations require specific adjustments to the multiplication process.
Engineering approach: an unsigned example
For example, suppose we want to multiply two unsignedSignedness
In computing, signedness is a property of data types representing numbers in computer programs. A numeric variable is signed if it can represent both positive and negative numbers, and unsigned if it can only represent non-negative numbers .As signed numbers can represent negative numbers, they...
eight bit integers together: a[7:0] and b[7:0]. We can produce eight partial products by performing eight one-bit multiplications, one for each bit in multiplicand a:
p1[7:0] = a[1] × b[7:0] = {8{a[1]}} & b[7:0]
p2[7:0] = a[2] × b[7:0] = {8{a[2]}} & b[7:0]
p3[7:0] = a[3] × b[7:0] = {8{a[3]}} & b[7:0]
p4[7:0] = a[4] × b[7:0] = {8{a[4]}} & b[7:0]
p5[7:0] = a[5] × b[7:0] = {8{a[5]}} & b[7:0]
p6[7:0] = a[6] × b[7:0] = {8{a[6]}} & b[7:0]
p7[7:0] = a[7] × b[7:0] = {8{a[7]}} & b[7:0]
where
To produce our product, we then need to add up all eight of our partial products, as shown here:
p0[7] p0[6] p0[5] p0[4] p0[3] p0[2] p0[1] p0[0]
+ p1[7] p1[6] p1[5] p1[4] p1[3] p1[2] p1[1] p1[0] 0
+ p2[7] p2[6] p2[5] p2[4] p2[3] p2[2] p2[1] p2[0] 0 0
+ p3[7] p3[6] p3[5] p3[4] p3[3] p3[2] p3[1] p3[0] 0 0 0
+ p4[7] p4[6] p4[5] p4[4] p4[3] p4[2] p4[1] p4[0] 0 0 0 0
+ p5[7] p5[6] p5[5] p5[4] p5[3] p5[2] p5[1] p5[0] 0 0 0 0 0
+ p6[7] p6[6] p6[5] p6[4] p6[3] p6[2] p6[1] p6[0] 0 0 0 0 0 0
+ p7[7] p7[6] p7[5] p7[4] p7[3] p7[2] p7[1] p7[0] 0 0 0 0 0 0 0
-------------------------------------------------------------------------------------------
P[15] P[14] P[13] P[12] P[11] P[10] P[9] P[8] P[7] P[6] P[5] P[4] P[3] P[2] P[1] P[0]
In other words, P[15:0] is produced by summing p0, p1 << 1, p2 << 2, and so forth, to produce our final unsigned 16-bit product.
Engineering approach: signed integers
If b had been a signedSignedness
In computing, signedness is a property of data types representing numbers in computer programs. A numeric variable is signed if it can represent both positive and negative numbers, and unsigned if it can only represent non-negative numbers .As signed numbers can represent negative numbers, they...
integer instead of an unsigned
Signedness
In computing, signedness is a property of data types representing numbers in computer programs. A numeric variable is signed if it can represent both positive and negative numbers, and unsigned if it can only represent non-negative numbers .As signed numbers can represent negative numbers, they...
integer, then the partial products would need to have been sign-extended up to the width of the product before summing. If a had been a signed integer, then partial product p7 would need to be subtracted from the final sum, rather than added to it.
The above array multiplier can be modified to support two's complement notation signed numbers by inverting several of the product terms and inserting a one to the left of the first partial product term:
1 -p0[7] p0[6] p0[5] p0[4] p0[3] p0[2] p0[1] p0[0]
-p1[7] +p1[6] +p1[5] +p1[4] +p1[3] +p1[2] +p1[1] +p1[0] 0
-p2[7] +p2[6] +p2[5] +p2[4] +p2[3] +p2[2] +p2[1] +p2[0] 0 0
-p3[7] +p3[6] +p3[5] +p3[4] +p3[3] +p3[2] +p3[1] +p3[0] 0 0 0
-p4[7] +p4[6] +p4[5] +p4[4] +p4[3] +p4[2] +p4[1] +p4[0] 0 0 0 0
-p5[7] +p5[6] +p5[5] +p5[4] +p5[3] +p5[2] +p5[1] +p5[0] 0 0 0 0 0
-p6[7] +p6[6] +p6[5] +p6[4] +p6[3] +p6[2] +p6[1] +p6[0] 0 0 0 0 0 0
1 +p7[7] -p7[6] -p7[5] -p7[4] -p7[3] -p7[2] -p7[1] -p7[0] 0 0 0 0 0 0 0
------------------------------------------------------------------------------------------------------------
P[15] P[14] P[13] P[12] P[11] P[10] P[9] P[8] P[7] P[6] P[5] P[4] P[3] P[2] P[1] P[0]
Do not be misled by the minus sign (-) notation above. It does not mean arithmetic negation ( -(7) = -7), but instead binary complementation, more commonly denoted
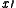(read x prime), 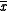(x bar) or ~ (tilde x), achieved by flipping all the bits. In two's complement to get the negation of a number, you complement the number then add 1, so they are NOT equivalent.There are a lot of simplifications in the bit array above that are not shown and are not obvious. The sequences of one complemented bit followed by noncomplemented bits are implementing a two's complement trick to avoid sign extension. The sequence of p7 (noncomplemented bit followed by all complemented bits) is because we're subtracting this term so they were all negated to start out with (and a 1 was added in the least significant position). For both types of sequences, the last bit is flipped and an implicit -1 should be added directly below the MSB. When the +1 from the two's complement negation for p7 in bit position 0 (LSB) and all the -1's in bit columns 7 through 14 (where each of the MSBs are located) are added together, they can be simplified to the single 1 that "magically" is floating out to the left. For an explanation and proof of why flipping the MSB saves us the sign extension, see a computer arithmetic book .
Implementations
Older multiplier architectures employed a shifter and accumulator to sum each partial product, often one partial product per cycle, trading off speed for die area. Modern multiplier architectures use the Baugh–Wooley algorithm, Wallace treeWallace tree
A Wallace tree is an efficient hardware implementation of a digital circuit that multiplies two integers, devised by an Australian Computer Scientist Chris Wallace in 1964.The Wallace tree has three steps:...
s, or Dadda multiplier
Dadda multiplier
The Dadda multiplier is a hardware multiplier design invented by computer scientist Luigi Dadda in 1965. It is similar to the Wallace multiplier, but it is slightly faster and requires fewer gates .In fact, Dadda and Wallace multipliers have the same 3 steps:# Multiply each bit of one of the...
s to add the partial products together in a single cycle. The performance of the Wallace tree
Wallace tree
A Wallace tree is an efficient hardware implementation of a digital circuit that multiplies two integers, devised by an Australian Computer Scientist Chris Wallace in 1964.The Wallace tree has three steps:...
implementation is sometimes improved by modified Booth encoding one of the two multiplicands, which reduces the number of partial products that must be summed.
See also
- Booth's multiplication algorithmBooth's multiplication algorithmBooth's multiplication algorithm is a multiplication algorithm that multiplies two signed binary numbers in two's complement notation. The algorithm was invented by Andrew Donald Booth in 1950 while doing research on crystallography at Birkbeck College in Bloomsbury, London...
- Fused multiply–add
- Wallace treeWallace treeA Wallace tree is an efficient hardware implementation of a digital circuit that multiplies two integers, devised by an Australian Computer Scientist Chris Wallace in 1964.The Wallace tree has three steps:...
- BKM algorithmBKM algorithmThe BKM algorithm is a shift-and-add algorithm for computing elementary functions, first published in 1994 by J.C. Bajard, S. Kla, and J.M. Muller. BKM is based on computing complex logarithms and exponentials using a method similar to the algorithm Henry Briggs used to compute logarithms...
for complex logarithms and exponentials - Kochanski multiplicationKochanski multiplicationKochanski multiplication is an algorithm that allows modular arithmetic to be performed efficiently when the modulus is large...
for modularModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
multiplication
External links
- Multiplier Designs targeted at FPGAs
- Self-clocking Multiplier using TTL
- Binary Multiplier circuit using Half -Adders and digital gates.