Bing metrization theorem
Encyclopedia
In topology
, the Bing metrization theorem, named after R. H. Bing, characterizes when a topological space
is metrizable. The theorem states that a topological space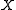
is metrizable if and only if it is regular
and T0 and has a σ-discrete basis. A family of sets is called σ-discrete when it is a union of countably many discrete collections, where a family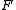
of subsets of a space 
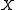is called discrete, when every point of 
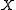has a neighborhood that intersects at most one member of 
.
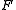Unlike the Urysohn's metrization theorem
which provides a sufficient condition for metrization, this theorem provides both a necessary and sufficient condition for a topological space
to be metrizable.
The theorem was proven by Bing
in 1951 and was an independent discovery with the Nagata-Smirnov metrization
theorem that was proved independently by both Nagata (1950) and Smirnov (1951). Both theorems are often merged in the Bing-Nagata-Smirnov metrization theorem. It is a common tool to prove other metrization theorem
s, e.g. the Moore metrization theorem: a collectionwise normal
, Moore space
is metrizable, is a direct consequence.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the Bing metrization theorem, named after R. H. Bing, characterizes when a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is metrizable. The theorem states that a topological space
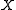is metrizable if and only if it is regularRegular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
and T0 and has a σ-discrete basis. A family of sets is called σ-discrete when it is a union of countably many discrete collections, where a family
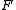of subsets of a space 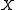is called discrete, when every point of 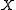has a neighborhood that intersects at most one member of 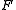.Unlike the Urysohn's metrization theorem
Metrization theorem
In topology and related areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space is said to be metrizable if there is a metricd\colon X \times X \to [0,\infty)...
which provides a sufficient condition for metrization, this theorem provides both a necessary and sufficient condition for a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
to be metrizable.
The theorem was proven by Bing
RH Bing
R. H. Bing was an American mathematician who worked mainly in the areas of geometric topology and continuum theory...
in 1951 and was an independent discovery with the Nagata-Smirnov metrization
Nagata–Smirnov metrization theorem
The Nagata–Smirnov metrization theorem in topology characterizes when a topological space is metrizable. The theorem states that a topological space X is metrizable if and only if it is regular and Hausdorff and has a countably locally finite basis.Unlike Urysohn's metrization theorem, which...
theorem that was proved independently by both Nagata (1950) and Smirnov (1951). Both theorems are often merged in the Bing-Nagata-Smirnov metrization theorem. It is a common tool to prove other metrization theorem
Metrization theorem
In topology and related areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space is said to be metrizable if there is a metricd\colon X \times X \to [0,\infty)...
s, e.g. the Moore metrization theorem: a collectionwise normal
Collectionwise normal
In mathematics, a topological space X is called collectionwise normal if for every discrete family Fi of closed subsets of X there exists a pairwise disjoint family of open sets Ui , such that Fi ⊂ Ui...
, Moore space
Moore space (topology)
In mathematics, more specifically point-set topology, a Moore space is a developable regular Hausdorff space. Equivalently, a topological space X is a Moore space if the following conditions hold:...
is metrizable, is a direct consequence.