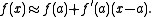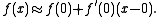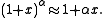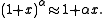Binomial approximation
Encyclopedia
The binomial approximation is useful for approximately calculating powers
of numbers close to 1. It states that if is a real number
is a real number
close to 0 and is a real number, then
is a real number, then
This approximation can be obtained by using the binomial theorem
and ignoring the terms beyond the first two.
The left-hand side of this relation is always greater than or equal to the right-hand side for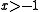 and
and  a non-negative integer, by Bernoulli's inequality
a non-negative integer, by Bernoulli's inequality
.
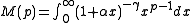
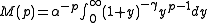
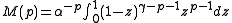
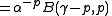
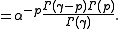
Using the inverse Mellin transform
:
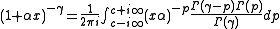
Closing this integral to the left, which converges for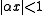 , we get:
, we get:
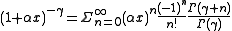
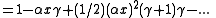
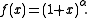
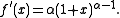
When x = 0:
Using linear approximation: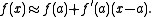
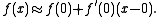
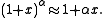
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of numbers close to 1. It states that if
 is a real number
is a real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
close to 0 and
 is a real number, then
is a real number, thenThis approximation can be obtained by using the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
and ignoring the terms beyond the first two.
The left-hand side of this relation is always greater than or equal to the right-hand side for
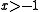 and
and  a non-negative integer, by Bernoulli's inequality
a non-negative integer, by Bernoulli's inequalityBernoulli's inequality
In real analysis, Bernoulli's inequality is an inequality that approximates exponentiations of 1 + x.The inequality states that^r \geq 1 + rx\!...
.
Derivation using Mellin Transform
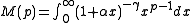
- Let
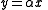
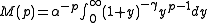
- Let y=z/(1-z)
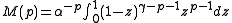
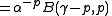
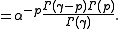
Using the inverse Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
:
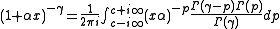
Closing this integral to the left, which converges for
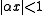 , we get:
, we get: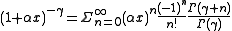
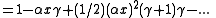
Derivation using Linear Approximation
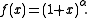
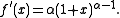
When x = 0:

Using linear approximation: