Birkhoff interpolation
Encyclopedia
In mathematics
, Birkhoff interpolation is an extension of polynomial interpolation
. It refers to the problem finding a polynomial p of degree d such that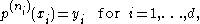
where the data points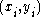
and the nonnegative integers 
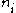are given. It differs from Hermite interpolation
in that it is possible to specify derivatives of p at some points without specifying the lower derivatives or the polynomial itself. The name refers to George David Birkhoff
, who first studied the problem in .
In contrast to Lagrange interpolation and Hermite interpolation, a Birkhoff interpolation problem does not always have a unique solution. For instance, there is no quadratic polynomial p such that p(−1) = p(1) = 0 and p′(0) = 1. On the other hand, the Birkhoff interpolation problem where the values of p′(−1), p(0) and p′(1) are given always has a unique solution .
An important problem in the theory of Birkhoff interpolation is to classify those problems that have a unique solution. formulates the problem as follows. Let d denote the number of conditions (as above) and let k be the number of interpolation points. Given an d-by-k matrix E, all of whose entries are either 0 or 1, such that exactly d entries are 1. Then the corresponding problem is to determine p such that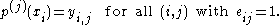
The matrix E is called the incidence matrix. For example, the incidence matrices for the interpolation problems mentioned in the previous paragraph are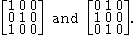
The question now becomes: does a Birkhoff interpolation problem with a given incidence matrix have a unique solution for any choice of the interpolation points?
The case with k = 2 interpolation points was tackled by . Let Sm denote the sum of the entries in the first m columns of the incidence matrix: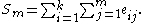
Then the Birkhoff interpolation problem with k = 2 has a unique solution if and only if Sm ≥ m for all m. showed that this is a necessary condition for all values of k.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Birkhoff interpolation is an extension of polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
. It refers to the problem finding a polynomial p of degree d such that
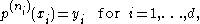
where the data points
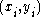and the nonnegative integers 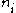are given. It differs from Hermite interpolationHermite interpolation
In numerical analysis, Hermite interpolation, named after Charles Hermite, is a method of interpolating data points as a polynomial function. The generated Hermite polynomial is closely related to the Newton polynomial, in that both are derived from the calculation of divided differences.Unlike...
in that it is possible to specify derivatives of p at some points without specifying the lower derivatives or the polynomial itself. The name refers to George David Birkhoff
George David Birkhoff
-External links:* − from National Academies Press, by Oswald Veblen....
, who first studied the problem in .
In contrast to Lagrange interpolation and Hermite interpolation, a Birkhoff interpolation problem does not always have a unique solution. For instance, there is no quadratic polynomial p such that p(−1) = p(1) = 0 and p′(0) = 1. On the other hand, the Birkhoff interpolation problem where the values of p′(−1), p(0) and p′(1) are given always has a unique solution .
An important problem in the theory of Birkhoff interpolation is to classify those problems that have a unique solution. formulates the problem as follows. Let d denote the number of conditions (as above) and let k be the number of interpolation points. Given an d-by-k matrix E, all of whose entries are either 0 or 1, such that exactly d entries are 1. Then the corresponding problem is to determine p such that
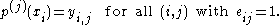
The matrix E is called the incidence matrix. For example, the incidence matrices for the interpolation problems mentioned in the previous paragraph are
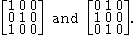
The question now becomes: does a Birkhoff interpolation problem with a given incidence matrix have a unique solution for any choice of the interpolation points?
The case with k = 2 interpolation points was tackled by . Let Sm denote the sum of the entries in the first m columns of the incidence matrix:
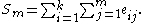
Then the Birkhoff interpolation problem with k = 2 has a unique solution if and only if Sm ≥ m for all m. showed that this is a necessary condition for all values of k.