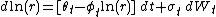Black–Karasinski model
Encyclopedia
In financial mathematics, the Black–Karasinski model is a mathematical model
of the term structure of interest rate
s; see short rate model
. It is a one-factor model as it describes interest rate movements as driven by a single source of randomness.
It belongs to the class of no-arbitrage models, i.e. it can fit today's zero coupon bond
prices, and in its most general form, today's prices for a set of caps, floors or European swaption
s. The model was introduced by Fischer Black
and Piotr Karasinski
in 1991.
):
where dWt is a standard Brownian motion
. The model implies a log-normal distribution for the short rate and therefore the expected value
of the money-market account is infinite for any maturity.
In the original article by Fischer Black and Piotr Karasinski the model was implemented using a binomial tree
with variable spacing, but a trinomial tree
implementation is more common in practice.
s such as American and Bermudan bond options and swaptions, once its parameters have been calibrated to the current term structure of interest rates and to the prices or implied volatilities of caps, floors or European swaptions.
No closed form solutions exist for the prices of bonds and of European bond options, hence numerical methods (usually trees) are used in the calibration stage as well as for pricing exotic interest rate derivatives.
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
of the term structure of interest rate
Interest rate
An interest rate is the rate at which interest is paid by a borrower for the use of money that they borrow from a lender. For example, a small company borrows capital from a bank to buy new assets for their business, and in return the lender receives interest at a predetermined interest rate for...
s; see short rate model
Short rate model
In the context of interest rate derivatives, a short-rate model is a mathematical model that describes the future evolution of interest rates by describing the future evolution of the short rate, usually written r_t \,.-The short rate:...
. It is a one-factor model as it describes interest rate movements as driven by a single source of randomness.
It belongs to the class of no-arbitrage models, i.e. it can fit today's zero coupon bond
Zero coupon bond
A zero-coupon bond is a bond bought at a price lower than its face value, with the face value repaid at the time of maturity. It does not make periodic interest payments, or have so-called "coupons," hence the term zero-coupon bond. When the bond reaches maturity, its investor receives its par ...
prices, and in its most general form, today's prices for a set of caps, floors or European swaption
Swaption
A swaption is an option granting its owner the right but not the obligation to enter into an underlying swap. Although options can be traded on a variety of swaps, the term "swaption" typically refers to options on interest rate swaps....
s. The model was introduced by Fischer Black
Fischer Black
Fischer Sheffey Black was an American economist, best known as one of the authors of the famous Black–Scholes equation.-Background:...
and Piotr Karasinski
Piotr Karasinski
Piotr Karasinski is a pioneering quantitative analyst, best known for the Black-Karasinski short rate model which he co-developed with the late Fischer Black. He is currently Senior Advisor at the European Bank for Reconstruction and Development. His contributions to quantitative finance include...
in 1991.
Model
The main state variable of the model is the short rate, which is assumed to follow the stochastic differential equation (under the risk-neutral measureRisk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
):
where dWt is a standard Brownian motion
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
. The model implies a log-normal distribution for the short rate and therefore the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the money-market account is infinite for any maturity.
In the original article by Fischer Black and Piotr Karasinski the model was implemented using a binomial tree
Binomial options pricing model
In finance, the binomial options pricing model provides a generalizable numerical method for the valuation of options. The binomial model was first proposed by Cox, Ross and Rubinstein in 1979. Essentially, the model uses a “discrete-time” model of the varying price over time of the underlying...
with variable spacing, but a trinomial tree
Trinomial Tree
The Trinomial tree is a lattice based computational model used in financial mathematics to price options. It was developed by Phelim Boyle in 1986. It is an extension of the Binomial options pricing model, and is conceptually similar...
implementation is more common in practice.
Applications
The model is used mainly for the pricing of exotic interest rate derivativeInterest rate derivative
An interest rate derivative is a derivative where the underlying asset is the right to pay or receive a notional amount of money at a given interest rate...
s such as American and Bermudan bond options and swaptions, once its parameters have been calibrated to the current term structure of interest rates and to the prices or implied volatilities of caps, floors or European swaptions.
No closed form solutions exist for the prices of bonds and of European bond options, hence numerical methods (usually trees) are used in the calibration stage as well as for pricing exotic interest rate derivatives.
External links
- Tutorial: Black-Karasinski Process Ludovic Dubrana