
Blaschke selection theorem
Encyclopedia
The Blaschke selection theorem is a result in topology
and convex geometry
about sequence
s of convex set
s. Specifically, given a sequence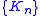 of convex sets contained in a bounded set, the theorem guarantees the existence of a subsequence
of convex sets contained in a bounded set, the theorem guarantees the existence of a subsequence  and a convex set
and a convex set  such that
such that  converges to
converges to  in the Hausdorff metric. The theorem is named for Wilhelm Blaschke
in the Hausdorff metric. The theorem is named for Wilhelm Blaschke
.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and convex geometry
Convex geometry
Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...
about sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s. Specifically, given a sequence
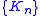 of convex sets contained in a bounded set, the theorem guarantees the existence of a subsequence
of convex sets contained in a bounded set, the theorem guarantees the existence of a subsequence  and a convex set
and a convex set  such that
such that  converges to
converges to  in the Hausdorff metric. The theorem is named for Wilhelm Blaschke
in the Hausdorff metric. The theorem is named for Wilhelm BlaschkeWilhelm Blaschke
Wilhelm Johann Eugen Blaschke was an Austro-Hungarian differential and integral geometer.His students included Shiing-Shen Chern, Luis Santaló, and Emanuel Sperner....
.
Alternate statements
- A succinct statement of the theorem is that a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
of convex bodies is locally compact.
- Using the Hausdorff metric on sets, every infinite collection of compact subsets of the unit ball has a limit point (and that limit point is itself a compact set).
Application
As an example of its use, the isoperimetric problem can be shown to have a solution. That is, there exists a curve of fixed length that encloses the maximum area possible. Other problems likewise can be shown to have a solution:- Lebesgue universal cover problem for a convex universal cover of minimal size for the collection of all sets in the plane of unit diameter,
- the maximum inclusion problem,
- and the Moser worm problem for a convex universal cover of minimal size for the collection of planar curves of unit length.

