
Bloch oscillations
Encyclopedia
Bloch oscillation is a phenomenon from solid state physics. It describes the oscillation of a particle (e.g. an electron
) confined in a periodic potential when a constant force is acting on it.
It was first pointed out by Bloch and Zener while studying the electrical properties of crystals. In particular, they predicted that the motion of electrons in a perfect crystal under the action of a constant electric field would be oscillatory instead of uniform. While in natural crystals this phenomenon is extremely hard to observe due to the scattering of electrons by lattice defects, it has been observed in semiconductor superlattices and in different physical systems such as cold atoms in an optical potential and ultrasmall Josephson junctions.
 ,
,
which has the solution
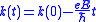 .
.
The velocity v of the electron is given by
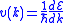 ,
,
where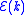 denotes the dispersion relation
denotes the dispersion relation
for the given energy band.
Suppose that the latter has the (tight-binding) form
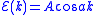 ,
,
where a is the lattice parameter and A is a constant. Then v(k) is given by
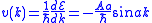 ,
,
and the electron position by
by
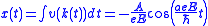 .
.
This shows that the electron oscillates in real space. The frequency of the oscillations is given by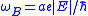 .
.
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
) confined in a periodic potential when a constant force is acting on it.
It was first pointed out by Bloch and Zener while studying the electrical properties of crystals. In particular, they predicted that the motion of electrons in a perfect crystal under the action of a constant electric field would be oscillatory instead of uniform. While in natural crystals this phenomenon is extremely hard to observe due to the scattering of electrons by lattice defects, it has been observed in semiconductor superlattices and in different physical systems such as cold atoms in an optical potential and ultrasmall Josephson junctions.
Derivation
The one-dimensional equation of motion for an electron in a constant electric field E is: ,
,which has the solution
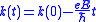 .
.The velocity v of the electron is given by
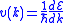 ,
,where
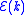 denotes the dispersion relation
denotes the dispersion relationDispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
for the given energy band.
Suppose that the latter has the (tight-binding) form
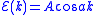 ,
,where a is the lattice parameter and A is a constant. Then v(k) is given by
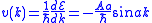 ,
,and the electron position
 by
by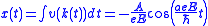 .
.This shows that the electron oscillates in real space. The frequency of the oscillations is given by
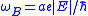 .
.

