Blom's scheme
Encyclopedia
Blom's scheme is a symmetric threshold key exchange
protocol in cryptography
. The scheme was proposed by the Swedish cryptographer Rolf Blom in a series of articles in the early 1980s .
A trusted party gives each participant a secret key and a public identifier, which enables any two participants to independently create a shared key for communicating. However, if an attacker can compromise the keys of at least k users, he can break the scheme and reconstruct every shared key. Blom's scheme is a form of threshold secret sharing.
Blom's scheme is currently used by the HDCP copy protection scheme to generate shared keys for high-definition content sources and receivers, such as HD DVD
players and high-definition television
s.
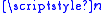users. Let Alice and Bob
be two users of the group.
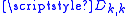over the finite field
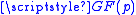, where p is a prime number. 
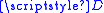is required when a new user is to be added to the key sharing group.
For example:
.
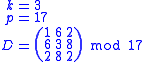
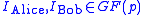For example:
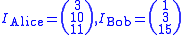
Trent then computes their private keys:
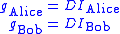
Using
as described above:
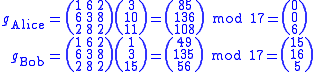
Each will use their private key to compute shared keys with other participants of the group.
and her private key 
.
She computes the shared key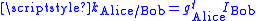
, where 
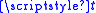denotes matrix transpose. Bob does the same, using his private key and her identifier, giving the same result:
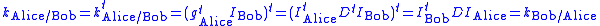
They will each generate their shared key as follows:
code (this error correction code requires only easily understandable mathematics and can be computed extremely quickly).
Key exchange
Key exchange is any method in cryptography by which cryptographic keys are exchanged between users, allowing use of a cryptographic algorithm....
protocol in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
. The scheme was proposed by the Swedish cryptographer Rolf Blom in a series of articles in the early 1980s .
A trusted party gives each participant a secret key and a public identifier, which enables any two participants to independently create a shared key for communicating. However, if an attacker can compromise the keys of at least k users, he can break the scheme and reconstruct every shared key. Blom's scheme is a form of threshold secret sharing.
Blom's scheme is currently used by the HDCP copy protection scheme to generate shared keys for high-definition content sources and receivers, such as HD DVD
HD DVD
HD DVD is a discontinued high-density optical disc format for storing data and high-definition video.Supported principally by Toshiba, HD DVD was envisioned to be the successor to the standard DVD format...
players and high-definition television
High-definition television
High-definition television is video that has resolution substantially higher than that of traditional television systems . HDTV has one or two million pixels per frame, roughly five times that of SD...
s.
The protocol
The key exchange protocol involves a trusted party (Trent) and a group of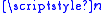 users. Let Alice and BobAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
be two users of the group.
Protocol setup
Trent chooses a random and secret symmetric matrix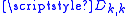 over the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
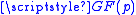, where p is a prime number. 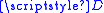is required when a new user is to be added to the key sharing group.For example:
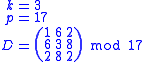
Inserting a new participant
New users Alice and Bob want to join the key exchanging group. Trent chooses public identifiers for each of them; i.e., k-element vectors: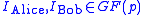.For example:
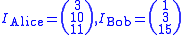
Trent then computes their private keys:
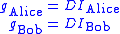
Using
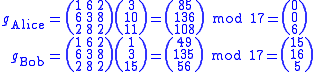
as described above:Each will use their private key to compute shared keys with other participants of the group.
Computing a shared key between Alice and Bob
Now Alice and Bob wish to communicate with one another. Alice has Bob's identifier and her private key 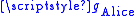.She computes the shared key
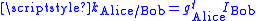, where 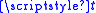denotes matrix transpose. Bob does the same, using his private key and her identifier, giving the same result: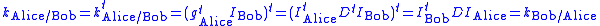They will each generate their shared key as follows:
Attack resistance
In order to ensure at least k keys must be compromised before every shared key can be computed by an attacker, identifiers must be k-linearly independent: all sets of k randomly selected user identifiers must be linearly independent. Otherwise, a group of malicious users can compute the key of any other member whose identifier is linearly dependent to theirs. To ensure this property, the identifiers shall be preferably chosen from a MDS-Code matrix (maximum distance separable error correction code matrix). The rows of the MDS-Matrix would be the identifiers of the users. A MDS-Code matrix can be chosen in practice using the code-matrix of the Reed–Solomon error correctionReed–Solomon error correction
In coding theory, Reed–Solomon codes are non-binary cyclic error-correcting codes invented by Irving S. Reed and Gustave Solomon. They described a systematic way of building codes that could detect and correct multiple random symbol errors...
code (this error correction code requires only easily understandable mathematics and can be computed extremely quickly).