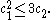Bogomolov–Miyaoka–Yau inequality
Encyclopedia
In mathematics, the Bogomolov–Miyaoka–Yau inequality is the inequality
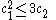
between Chern numbers of compact
complex surfaces
of general type. Its major interest is the way it restricts the possible topological types of the underlying real 4-manifold. It was proved independently by and , after and proved weaker versions with the constant 3 replaced by 8 and 4.
Borel
and Hirzebruch showed that the inequality is best possible by finding infinitely many cases where equality holds. The inequality is false in positive characteristic: and gave examples of surfaces in characteristic p, such as generalized Raynaud surfaces, for which it fails.
Let X be a compact complex surface of general type, and let c1 = c1(X) and c2 = c2(X) be the first and second Chern class
of the complex tangent bundle of the surface. Then
moreover if equality holds then X is a quotient of a ball. The latter statement is a consequence of Yau's differential geometric approach which is based on his resolution of the Calabi conjecture
.
Since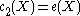
is the topological Euler characteristic
and by the Thom–Hirzebruch signature theorem
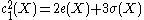where 
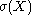is the signature of the intersection form
on the second cohomology, the Bogomolov–Miyaoka–Yau inequality can also be written as a restriction on the topological type of the surface of general type:
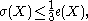
moreover if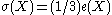
then the universal covering is a ball.
Together with the Noether inequality
the Bogomolov–Miyaoka–Yau inequality sets boundaries in the search for complex surfaces. Mapping out the topological types that are realized as complex surfaces is called geography of surfaces.
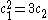, so that equality holds in the Bogomolov–Miyaoka–Yau inequality, then proved that X is isomorphic to a quotient of the unit ball in 
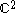by an infinite discrete group. Examples of surfaces satisfying this equality are hard to find. showed that there are infinitely many values of c = 3c2 for which a surface exists. found a fake projective plane
with c = 3c2 = 9, which is the minimum possible value because c + c2 is always divisible by 12, and showed that there are exactly 50 fake projective planes.
gave a method for finding examples, which in particular produced a surface X with c = 3c2 = 3254.
found a quotient of this surface with c = 3c2 = 45, and taking unbranched coverings of this quotient gives examples with c = 3c2 = 45k for any positive integer k.
found examples with c = 3c2 = 9n for every positive integer n.
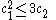
between Chern numbers of compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
complex surfaces
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
of general type. Its major interest is the way it restricts the possible topological types of the underlying real 4-manifold. It was proved independently by and , after and proved weaker versions with the constant 3 replaced by 8 and 4.
Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
and Hirzebruch showed that the inequality is best possible by finding infinitely many cases where equality holds. The inequality is false in positive characteristic: and gave examples of surfaces in characteristic p, such as generalized Raynaud surfaces, for which it fails.
Formulation of the inequality
The conventional formulation of the Bogomolov–Miyaoka–Yau inequality isLet X be a compact complex surface of general type, and let c1 = c1(X) and c2 = c2(X) be the first and second Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the complex tangent bundle of the surface. Then
moreover if equality holds then X is a quotient of a ball. The latter statement is a consequence of Yau's differential geometric approach which is based on his resolution of the Calabi conjecture
Calabi conjecture
In mathematics, the Calabi conjecture was a conjecture about the existence of good Riemannian metrics on complex manifolds, made by and proved by ....
.
Since
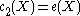is the topological Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
and by the Thom–Hirzebruch signature theorem
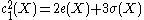where 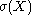is the signature of the intersection formIntersection form
Intersection form may refer to:*Intersection theory *intersection form...
on the second cohomology, the Bogomolov–Miyaoka–Yau inequality can also be written as a restriction on the topological type of the surface of general type:
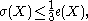
moreover if
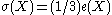then the universal covering is a ball.Together with the Noether inequality
Noether inequality
In mathematics, the Noether inequality, named after Max Noether, is a property of compact minimal complex surfaces that restricts the topological type of the underlying topological 4-manifold...
the Bogomolov–Miyaoka–Yau inequality sets boundaries in the search for complex surfaces. Mapping out the topological types that are realized as complex surfaces is called geography of surfaces.
Surfaces with c12 = 3c2
If X is a surface of general type with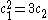, so that equality holds in the Bogomolov–Miyaoka–Yau inequality, then proved that X is isomorphic to a quotient of the unit ball in 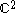by an infinite discrete group. Examples of surfaces satisfying this equality are hard to find. showed that there are infinitely many values of c = 3c2 for which a surface exists. found a fake projective planeFake projective plane
In mathematics, a fake projective plane is one of the 50 complex algebraic surfaces that have the same Betti numbers as the projective plane, but are not isomorphic to it. Such objects are always algebraic surfaces of general type....
with c = 3c2 = 9, which is the minimum possible value because c + c2 is always divisible by 12, and showed that there are exactly 50 fake projective planes.
gave a method for finding examples, which in particular produced a surface X with c = 3c2 = 3254.
found a quotient of this surface with c = 3c2 = 45, and taking unbranched coverings of this quotient gives examples with c = 3c2 = 45k for any positive integer k.
found examples with c = 3c2 = 9n for every positive integer n.