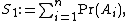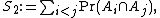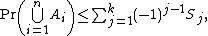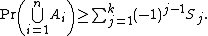Boole's inequality
Encyclopedia
In probability theory
, Boole's inequality, also known as the union bound, says that for any finite or countable set of event
s, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events. Boole's inequality is named after George Boole
.
Formally, for a countable set of events A1, A2, A3, ..., we have
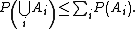
In measure-theoretic terms, Boole's inequality follows from the fact that a measure (and certainly any probability measure
) is σ-sub-additive.
and lower bound
s on the probability of finite unions of events. These bounds are known as Bonferroni inequalities, after Carlo Emilio Bonferroni
.
Define
and for 2 < k ≤ n,
where the summation is taken over all k-tuple
s of integer
s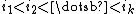 .
.
Then, for odd
k ≥ 1,
and for even
k ≥ 2,
Boole's inequality is recovered by setting k = 1.
When k = n, then equality holds and the resulting identity is the inclusion-exclusion principle
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Boole's inequality, also known as the union bound, says that for any finite or countable set of event
Event (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
s, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events. Boole's inequality is named after George Boole
George Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
.
Formally, for a countable set of events A1, A2, A3, ..., we have
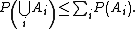
In measure-theoretic terms, Boole's inequality follows from the fact that a measure (and certainly any probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
) is σ-sub-additive.
Bonferroni inequalities
Boole's inequality may be generalised to find upperUpper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
and lower bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
s on the probability of finite unions of events. These bounds are known as Bonferroni inequalities, after Carlo Emilio Bonferroni
Carlo Emilio Bonferroni
Carlo Emilio Bonferroni was an Italian mathematician who worked on probability theory. Carlo Emilio Bonferroni was born in Bergamo on 28 January 1892 and died on 18 August 1960 in Firenze . He studied in Torino , held a post as assistant professor at the Turin Polytechnic, and in 1923 took up the...
.
Define
and for 2 < k ≤ n,
where the summation is taken over all k-tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s
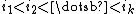 .
.Then, for odd
Even and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
k ≥ 1,
and for even
Even and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
k ≥ 2,
Boole's inequality is recovered by setting k = 1.
When k = n, then equality holds and the resulting identity is the inclusion-exclusion principle
Inclusion-exclusion principle
In combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
.