The Boolean model for a random subset of the plane (or higher dimensions, analogously) is one of the simplest and most tractable models in stochastic geometry

Stochastic geometry

In mathematics, stochastic geometry is the study of random spatial patterns. At the heart of the subject lies the study of random point patterns...

. Take a Poisson point process

Poisson process

A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...

 of rate in the plane and make each point be the center of a random set; the resulting union of overlapping sets is a realization of the Boolean model 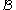. More precisely, the parameters are 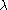and a probability distribution on compact sets; for each point of the Poisson point process we pick a set 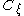from the distribution, and then define as the union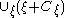
of translated sets.

To illustrate tractability with one simple formula, the mean density of equals 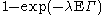where denotes the area of . The classical theory of stochastic geometry

Stochastic geometry

In mathematics, stochastic geometry is the study of random spatial patterns. At the heart of the subject lies the study of random point patterns...

 develops many further formulas – see

.

As related topics, the case of constant-sized discs is the basic model of continuum percolation

and the low-density Boolean models serve as a first-order approximations in the
study of extremes in many models
.