Boundary-layer thickness
Encyclopedia
This page describes some parameters used to measure the properties of boundary layers. Consider a stationary body with a turbulent flow moving around it, like the semi-infinite flat plate with air flowing over the top of the plate. At the solid walls of the body the fluid satisfies a no-slip boundary condition and has zero velocity, but as you move away from the wall, the velocity of the flow asymptotically approaches the free stream mean velocity. Therefore it is impossible to define a clear point at which the boundary layer becomes the free stream. The parameters below overcome this and allow the boundary layer to be measured.
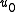. This distance is defined normal to the wall, and the point where the flow velocity is essentially that of the free stream is customarily defined as the point where: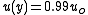
For laminar boundary layers over a flat plate, the Blasius solution
gives: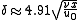
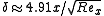
For turbulent boundary layers over a flat plate, the boundary layer thickness is given by: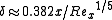
where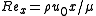
is the overall thickness (or height) of the boundary layer
is the kinematic viscosity
is the distance downstream from the start of the boundary layer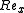
is the Reynolds Number
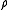is the density
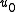is the freestream velocity
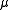is the dynamic viscosity
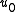to give the same flow rate as occurs between the surface and the reference plane in a real fluid.
In practical aerodynamics
, the displacement thickness essentially modifies the shape of a body immersed in a fluid to allow an inviscid solution. It is commonly used in aerodynamics to overcome the difficulty inherent in the fact that the fluid velocity in the boundary layer
approaches asymptotically to the free stream value as distance from the wall increases at any given location.
The definition of the displacement thickness for compressible flow is based on mass flow rate:
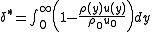
The definition for incompressible flow can be based on volumetric flow rate, as the density is constant:
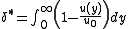
Where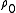
and 
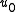are the density and velocity in the 'free stream' outside the boundary layer, and 
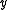is the coordinate normal to the wall.
For boundary layer calculations, the density and velocity at the edge of the boundary layer must be used, as there is no free stream. In the equations above,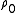
and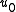 
are therefore replaced with 
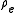and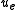 
.
The displacement thickness is used to calculate the boundary layer's shape factor.
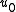to give the same total momentum as exists between the surface and the reference plane in a real fluid.
The definition of the momentum thickness for compressible flow is based on mass flow rate:
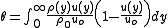
The definition for incompressible flow can be based on volumetric flow rate, as the density is constant:
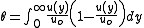
Where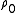
and 
are the density and velocity in the 'free stream' outside the boundary layer, and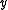 
is the coordinate normal to the wall.
For boundary layer calculations, the density and velocity at the edge of the boundary layer must be used, as there is no free stream. In the equations above,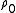
and 
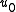are therefore replaced with 
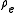and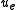 
.
For a flat plate at no angle of attack
with a laminar boundary layer, the Blasius solution gives
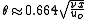
The influence of fluid viscosity
creates a wall shear stress
,
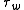, which extracts energy from the mean flow. The boundary layer can be considered to possess a total momentum flux deficit, due to the frictional dissipation
.
Other length scales describing viscous boundary layers include the energy thickness,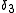
.
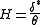
where H is the shape factor,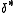
is the displacement thickness and θ is the momentum thickness. The higher the value of H, the stronger the adverse pressure gradient
. A high adverse pressure gradient can greatly reduce the Reynolds number at which transition into turbulence
may occur.
Conventionally, H=2.6 is typical of laminar flows, while H=1.3 is typical of turbulent flows.
99% Velocity thickness
The boundary layer thickness, δ, is the distance across a boundary layer from the wall to a point where the flow velocity has essentially reached the 'free stream' velocity,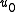. This distance is defined normal to the wall, and the point where the flow velocity is essentially that of the free stream is customarily defined as the point where: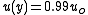For laminar boundary layers over a flat plate, the Blasius solution
Blasius boundary layer
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow U....
gives:
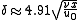
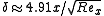
For turbulent boundary layers over a flat plate, the boundary layer thickness is given by:
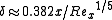
where
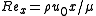
is the overall thickness (or height) of the boundary layer is the kinematic viscosity is the distance downstream from the start of the boundary layer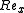 is the Reynolds Number 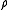is the density 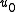is the freestream velocity 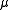is the dynamic viscosityDisplacement thickness
The displacement thickness, δ* or δ1 is the distance by which a surface would have to be moved in the direction parallel to its normal vector towards the reference plane in an inviscid fluid stream of velocity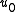 to give the same flow rate as occurs between the surface and the reference plane in a real fluid.In practical aerodynamics
Aerodynamics
Aerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
, the displacement thickness essentially modifies the shape of a body immersed in a fluid to allow an inviscid solution. It is commonly used in aerodynamics to overcome the difficulty inherent in the fact that the fluid velocity in the boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
approaches asymptotically to the free stream value as distance from the wall increases at any given location.
The definition of the displacement thickness for compressible flow is based on mass flow rate:
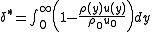
The definition for incompressible flow can be based on volumetric flow rate, as the density is constant:
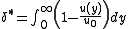
Where
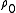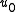and are the density and velocity in the 'free stream' outside the boundary layer, and 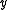is the coordinate normal to the wall.For boundary layer calculations, the density and velocity at the edge of the boundary layer must be used, as there is no free stream. In the equations above,
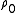and 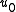are therefore replaced with 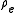and 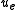.The displacement thickness is used to calculate the boundary layer's shape factor.
Momentum thickness
The momentum thickness, θ or δ2, is the distance by which a surface would have to be moved parallel to itself towards the reference plane in an inviscid fluid stream of velocity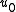 to give the same total momentum as exists between the surface and the reference plane in a real fluid.The definition of the momentum thickness for compressible flow is based on mass flow rate:
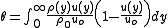
The definition for incompressible flow can be based on volumetric flow rate, as the density is constant:
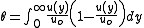
Where
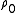and are the density and velocity in the 'free stream' outside the boundary layer, and 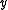is the coordinate normal to the wall.For boundary layer calculations, the density and velocity at the edge of the boundary layer must be used, as there is no free stream. In the equations above,
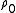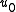and are therefore replaced with 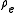and 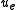.For a flat plate at no angle of attack
Angle of attack
Angle of attack is a term used in fluid dynamics to describe the angle between a reference line on a lifting body and the vector representing the relative motion between the lifting body and the fluid through which it is moving...
with a laminar boundary layer, the Blasius solution gives
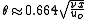
The influence of fluid viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
creates a wall shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
,
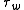, which extracts energy from the mean flow. The boundary layer can be considered to possess a total momentum flux deficit, due to the frictional dissipationDissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
.
Other length scales describing viscous boundary layers include the energy thickness,
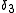.Shape factor
A shape factor is used in boundary layer flow to determine the nature of the flow.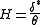where H is the shape factor,
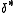is the displacement thickness and θ is the momentum thickness. The higher the value of H, the stronger the adverse pressure gradientPressure gradient
In atmospheric sciences , the pressure gradient is a physical quantity that describes in which direction and at what rate the pressure changes the most rapidly around a particular location. The pressure gradient is a dimensional quantity expressed in units of pressure per unit length...
. A high adverse pressure gradient can greatly reduce the Reynolds number at which transition into turbulence
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
may occur.
Conventionally, H=2.6 is typical of laminar flows, while H=1.3 is typical of turbulent flows.
Further Reading
- F.M. White, "Fluid Mechanics", McGraw-Hill, 5th Edition, 2003.
- B.R. Munson, D.F. Young and T.H. Okiishi, "Fundamentals of Fluid Mechanics", John Wiley, 4th Edition, 2002.
- B. Massey and J. Ward-Smith, "Mechanics of Fluids", Taylor and Francis, 8th Edition, 2006.