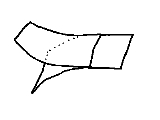
Branched surface
Encyclopedia
In mathematics
, a branched surface is type of topological space
. A small piece of an surface
looks topologically (i.e., up to
homeomorphism
) like ℝ²
. A small piece of a branched surface, on the other hand, might look like either of the following:
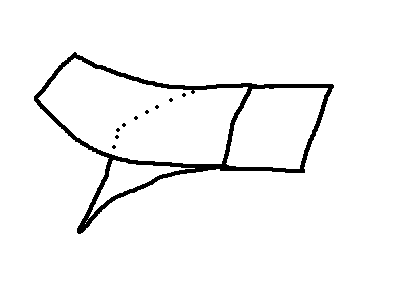 A branched manifold can have a weight assigned to various of its subspaces; if this is done, the space is often called a weighted branched manifold. Weights are non-negative real number
A branched manifold can have a weight assigned to various of its subspaces; if this is done, the space is often called a weighted branched manifold. Weights are non-negative real number
s and are assigned to subspaces N that satisfy the following:
That is, N is the space from one branching to the next. Weights are assigned so that any if a neighborhood of a point is the quotient space described above, then the sum of the weights of the two unidentified hyperplanes of that neighborhood is the weight of the identified hyperplane space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a branched surface is type of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. A small piece of an surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
looks topologically (i.e., up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
) like ℝ²
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. A small piece of a branched surface, on the other hand, might look like either of the following:
- ℝ²;
- the quotient spaceQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of two copies of ℝ² modulo the identification of a closed half-spaceHalf-spaceIn geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
of each with a closed half-space of the other. Needs work.

Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and are assigned to subspaces N that satisfy the following:
- N is open.
- N does not include any points whose only neighborhoods are the quotient space described above.
- N is maximal with respect to the above two conditions.
That is, N is the space from one branching to the next. Weights are assigned so that any if a neighborhood of a point is the quotient space described above, then the sum of the weights of the two unidentified hyperplanes of that neighborhood is the weight of the identified hyperplane space.

