
Burrows-Abadi-Needham logic
Encyclopedia
Burrows–Abadi–Needham logic (also known as the BAN logic) is a set of rules for defining and analyzing information exchange protocols. Specifically, BAN logic helps its users determine whether exchanged information is trustworthy, secured against eavesdropping, or both. BAN logic starts with the assumption that all information exchanges happen on media vulnerable to tampering and public monitoring. This has evolved into the popular security mantra, "Don't trust the network."
A typical BAN logic sequence includes three steps:
BAN logic uses postulates and definition
s – like all axiomatic system
s – to analyze authentication
protocols. Use of the BAN logic often accompanies a security protocol notation
formulation of a protocol and is sometimes given in papers.
BAN logic inspired many other similar formalisms, such as GNY logic. Some of these try to repair one weakness of BAN logic: the lack of a good semantics with a clear meaning in terms of knowledge and possible universes.
and K is an encryption key):
The meaning of these definitions is captured in a series of postulates:
P must believe that X is fresh here. If X is not known to be fresh, then it might be an obsolete message, replayed by an attacker.
Using this notation, the assumptions behind an authentication protocol
can be formalized. Using the postulates, one can prove that certain
agents believe that they can communicate using certain keys. If the
proof fails, the point of failure usually suggests an attack which
compromises the protocol.
— allows two agents, A and B, to establish secure communications, using a trusted authentication server, S, and synchronized clocks all around. Using standard notation the protocol can be specified as follows:
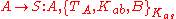
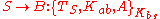
Agents A and B are equipped with keys Kas and Kbs, respectively, for communicating securely with S. So we have assumptions:
Agent A wants to initiate a secure conversation with B. It therefore invents a key, Kab, which it will use to communicate with B. A believes that this key is secure, since it made up the key itself:
B is willing to accept this key, as long as it is sure that it came from A:
Moreover, B is willing to trust S to accurately relay keys from A:
That is, if B believes that S believes that A wants to use a particular key to communicate with B, then B will trust S and believe it also.
The goal is to have
A reads the clock, obtaining the current time t, and sends the following message:
That is, it sends its chosen session key and the current time to S, encrypted with its private authentication server key Kas.
Since S believes that key(Kas, A↔S), and S sees {t, key(Kab, A↔B)}Kas,
then S concludes that A actually said {t, key(Kab, A↔B)}. (In particular, S believes that the message was not manufactured out of whole cloth by some attacker.)
Since the clocks are synchronized, we can assume
Since S believes fresh(t) and S believes A said {t, key(Kab, A↔B)},
S believes that A actually believes that key(Kab, A↔B). (In particular, S believes that the message was not replayed by some attacker who captured it at some time in the past.)
S then forwards the key to B:
Because message 2 is encrypted with Kbs, and B
believes key(Kbs, B↔S), B now believes that S
said {t, A, A believes key(Kab, A↔B)}.
Because the clocks are synchronized, B believes fresh(t), and so
fresh(A believes key(Kab, A↔B)). Because B
believes that S' s statement is fresh, B believes that S believes that
(A believes key(Kab, A↔B)). Because B
believes that S is authoritative about what A believes, B believes
that (A believes key(Kab, A↔B)). Because B
believes that A is authoritative about session keys between A and B, B
believes key(Kab, A↔B). B can now contact A
directly, using Kab as a secret session key.
Now let's suppose that we abandon the assumption that the clocks are
synchronized. In that case, S gets message 1 from A with {t,
key(Kab, A↔B)}, but it can no longer conclude
that t is fresh. It knows that A sent this message at some time
in the past (because it is encrypted with Kas)
but not that this is a recent message, so S doesn't believe that A
necessarily wants to continue to use the key
Kab. This points directly at an attack on the
protocol: An attacker who can capture messages can guess one of the
old session keys Kab. (This might take a long
time.) The attacker then replays the old {t,
key(Kab, A↔B)} message, sending it to S. If
the clocks aren't synchronized (perhaps as part of the same attack), S might
believe this old message and request that B use the old, compromised key
over again.
The original Logic of Authentication paper (linked below) contains this example and many others, including analyses of the Kerberos handshake protocol, and two versions of the Andrew Project
RPC handshake (one of which is defective).
A typical BAN logic sequence includes three steps:
- Verification of message origin
- Verification of message freshness
- Verification of the origin's trustworthiness.
BAN logic uses postulates and definition
Definition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
s – like all axiomatic system
Axiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
s – to analyze authentication
Authentication
Authentication is the act of confirming the truth of an attribute of a datum or entity...
protocols. Use of the BAN logic often accompanies a security protocol notation
Security protocol notation
In cryptography, security protocol notation is a way of expressing a protocol of correspondence between entities of a dynamic system, such as a computer network...
formulation of a protocol and is sometimes given in papers.
Language type and alternatives
BAN logic, and logics in the same family, are decidable: there exists an algorithm taking BAN hypotheses and a purported conclusion, and that answers whether or not the conclusion is derivable from the hypotheses. The proposed algorithms use a variant of magic sets (Monniaux, 1999).BAN logic inspired many other similar formalisms, such as GNY logic. Some of these try to repair one weakness of BAN logic: the lack of a good semantics with a clear meaning in terms of knowledge and possible universes.
Basic rules
The definitions and their implications are below (P and Q are network agents, X is a message,and K is an encryption key):
- P believes X: P acts as if X is true, and may assert X in other messages.
- P has jurisdiction over X: P
' s beliefs about X should be trusted. - P said X: At one time, P transmitted (and believed) message X, although P might no longer believe X.
- P sees X: P receives message X, and can read and repeat X.
- {X}K: X is encrypted with key K.
- fresh(X): X has not previously been sent in any message.
- key(K, P↔Q): P and Q may communicate with shared key K
The meaning of these definitions is captured in a series of postulates:
- If P believes key(K, P↔Q), and P sees {X}K, then P believes (Q said X)
- If P believes (Q said X) and P believes fresh(X), then P believes (Q believes X).
P must believe that X is fresh here. If X is not known to be fresh, then it might be an obsolete message, replayed by an attacker.
- If P believes (Q has jurisdiction over X) and P believes (Q believes X), then P believes X
- There are several other technical postulates having to do with composition of messages. For example, if P believes that Q said <X, Y>, the concatenation of X and Y, then P also believes that Q said X, and P also believes that Q said Y.
Using this notation, the assumptions behind an authentication protocol
can be formalized. Using the postulates, one can prove that certain
agents believe that they can communicate using certain keys. If the
proof fails, the point of failure usually suggests an attack which
compromises the protocol.
BAN logic analysis of the Wide Mouth Frog protocol
A very simple protocol — the Wide Mouth Frog protocolWide Mouth Frog protocol
The Wide-Mouth Frog protocol is a computer network authentication protocol designed for use on insecure networks . It allows individuals communicating over a network to prove their identity to each other while also preventing eavesdropping or replay attacks, and provides for detection of...
— allows two agents, A and B, to establish secure communications, using a trusted authentication server, S, and synchronized clocks all around. Using standard notation the protocol can be specified as follows:
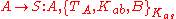
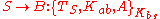
Agents A and B are equipped with keys Kas and Kbs, respectively, for communicating securely with S. So we have assumptions:
- A believes key(Kas, A↔S)
- S believes key(Kas, A↔S)
- B believes key(Kbs, B↔S)
- S believes key(Kbs, B↔S)
Agent A wants to initiate a secure conversation with B. It therefore invents a key, Kab, which it will use to communicate with B. A believes that this key is secure, since it made up the key itself:
- A believes key(Kab, A↔B)
B is willing to accept this key, as long as it is sure that it came from A:
- B believes (A has jurisdiction over key(K, A↔B))
Moreover, B is willing to trust S to accurately relay keys from A:
- B believes (S has jurisdiction over (A believes key(K, A↔B)))
That is, if B believes that S believes that A wants to use a particular key to communicate with B, then B will trust S and believe it also.
The goal is to have
- B believes key(Kab, A↔B)
A reads the clock, obtaining the current time t, and sends the following message:
- 1 A->S: {t, key(Kab, A↔B)}Kas
That is, it sends its chosen session key and the current time to S, encrypted with its private authentication server key Kas.
Since S believes that key(Kas, A↔S), and S sees {t, key(Kab, A↔B)}Kas,
then S concludes that A actually said {t, key(Kab, A↔B)}. (In particular, S believes that the message was not manufactured out of whole cloth by some attacker.)
Since the clocks are synchronized, we can assume
- S believes fresh(t)
Since S believes fresh(t) and S believes A said {t, key(Kab, A↔B)},
S believes that A actually believes that key(Kab, A↔B). (In particular, S believes that the message was not replayed by some attacker who captured it at some time in the past.)
S then forwards the key to B:
- 2 S->B: {t, A, A believes key(Kab, A↔B)}Kbs
Because message 2 is encrypted with Kbs, and B
believes key(Kbs, B↔S), B now believes that S
said {t, A, A believes key(Kab, A↔B)}.
Because the clocks are synchronized, B believes fresh(t), and so
fresh(A believes key(Kab, A↔B)). Because B
believes that S
(A believes key(Kab, A↔B)). Because B
believes that S is authoritative about what A believes, B believes
that (A believes key(Kab, A↔B)). Because B
believes that A is authoritative about session keys between A and B, B
believes key(Kab, A↔B). B can now contact A
directly, using Kab as a secret session key.
Now let's suppose that we abandon the assumption that the clocks are
synchronized. In that case, S gets message 1 from A with {t,
key(Kab, A↔B)}, but it can no longer conclude
that t is fresh. It knows that A sent this message at some time
in the past (because it is encrypted with Kas)
but not that this is a recent message, so S doesn't believe that A
necessarily wants to continue to use the key
Kab. This points directly at an attack on the
protocol: An attacker who can capture messages can guess one of the
old session keys Kab. (This might take a long
time.) The attacker then replays the old {t,
key(Kab, A↔B)} message, sending it to S. If
the clocks aren't synchronized (perhaps as part of the same attack), S might
believe this old message and request that B use the old, compromised key
over again.
The original Logic of Authentication paper (linked below) contains this example and many others, including analyses of the Kerberos handshake protocol, and two versions of the Andrew Project
Andrew Project
The Andrew Project was a distributed computing environment developed at Carnegie Mellon University beginning in 1982. It was an ambitious project for its time and resulted in an unprecedentedly vast and accessible university computing infrastructure....
RPC handshake (one of which is defective).
External links
- A Logic of Authentication (mirror), the original paper by BurrowsMichael BurrowsMichael Burrows is widely known as the creator of the Burrows–Wheeler transform. He also was, with Louis Monier, one of the two main creators of AltaVista. He did his first degree in Electronic Engineering with Computer Science at University College London...
, AbadiMartín AbadiMartín Abadi is an argentinian computer scientist, currently working at the University of California, Santa Cruz and Microsoft Research. He earned his Ph.D...
, and NeedhamRoger NeedhamRoger Michael Needham, CBE, FRS, FREng was a British computer scientist.-Early life:He attended Doncaster Grammar School for Boys in Doncaster ....
. - Source: The Burrows–Abadi–Needham logic
- BAN logic in context, from UT Austin CS (PDF)

