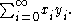C space
Encyclopedia
In the mathematical
field of functional analysis
, the space denoted by c is the vector space
of all convergent sequences (xn) of real number
s or complex number
s. When equipped with the uniform norm:
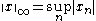
the space c becomes a Banach space
. It is a closed
linear subspace
of the space of bounded sequences, ℓ∞
, and contains as a closed subspace the Banach space c0 of sequences converging to zero. The dual
of c is isometrically isomorphic to ℓ1, as is that of c0. In particular, neither c nor c0 is reflexive
.
In the first case, the isomorphism of ℓ1 with c* is given as follows. If (x0,x1,...) ∈ ℓ1, then the pairing with an element (y1,y2,...) in c is given by
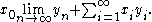
This is the Riesz representation theorem
on the ordinal ω.
For c0, the pairing between (xi) in ℓ1 and (yi) in c0 is given by
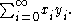
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the space denoted by c is the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of all convergent sequences (xn) of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. When equipped with the uniform norm:
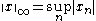
the space c becomes a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. It is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of the space of bounded sequences, ℓ∞
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, and contains as a closed subspace the Banach space c0 of sequences converging to zero. The dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of c is isometrically isomorphic to ℓ1, as is that of c0. In particular, neither c nor c0 is reflexive
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
.
In the first case, the isomorphism of ℓ1 with c* is given as follows. If (x0,x1,...) ∈ ℓ1, then the pairing with an element (y1,y2,...) in c is given by
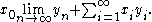
This is the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
on the ordinal ω.
For c0, the pairing between (xi) in ℓ1 and (yi) in c0 is given by