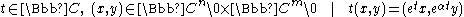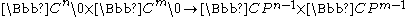Calabi–Eckmann manifold
Encyclopedia
In complex geometry
, a part of mathematics, a Calabi–Eckmann manifold (or, often, Calabi–Eckmann space), named after Eugenio Calabi
and Beno Eckmann
, is a complex
, homogeneous
, non-Kaehler manifold, homeomorphic to a product of two odd-dimensional spheres of dimension ≥ 3.
The Calabi–Eckmann manifold is constructed as follows. Consider the space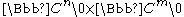
, m,n > 1, equipped with an action of a group 
:
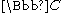where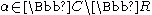
is a fixed complex number. It is easy to check that this action is free and proper, and the corresponding orbit space M is homeomorphic to S2n−1 × S2m−1. Since M is a quotient space of a holomorphic action, it is also a complex manifold. It is obviously homogeneous, with a transitive holomorphic action of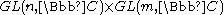 
A Calabi–Eckmann manifold M is non-Kaehler, because
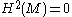. It is the simplest example of a non-Kaehler
manifold which is simply connected (in dimension 2, all
simply connected compact complex manifolds are Kaehler).
The natural projection
induces a holomorphic map from the corresponding Calabi–Eckmann manifold M to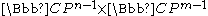
. The fiber of this map is an elliptic curve T, obtained as a quotient of 
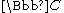by the lattice 
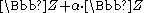. This makes M into a principal
T-bundle.
Calabi and Eckmann discovered these manifolds in 1953.
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
, a part of mathematics, a Calabi–Eckmann manifold (or, often, Calabi–Eckmann space), named after Eugenio Calabi
Eugenio Calabi
Eugenio Calabi is a Italian American mathematician and professor emeritus at the University of Pennsylvania, specializing in differential geometry, partial differential equations and their applications....
and Beno Eckmann
Beno Eckmann
Beno Eckmann was a Swiss mathematician who was a student of Heinz Hopf.Born in Bern, Eckmann received his master's degree from Eidgenössische Technische Hochschule Zürich in 1931. Later he studied there under Heinz Hopf, obtaining his Ph.D. in 1941...
, is a complex
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
, homogeneous
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
, non-Kaehler manifold, homeomorphic to a product of two odd-dimensional spheres of dimension ≥ 3.
The Calabi–Eckmann manifold is constructed as follows. Consider the space
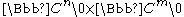, m,n > 1, equipped with an action of a group :
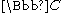where
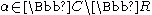is a fixed complex number. It is easy to check that this action is free and proper, and the corresponding orbit space M is homeomorphic to S2n−1 × S2m−1. Since M is a quotient space of a holomorphic action, it is also a complex manifold. It is obviously homogeneous, with a transitive holomorphic action of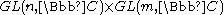 A Calabi–Eckmann manifold M is non-Kaehler, because
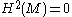. It is the simplest example of a non-Kaehlermanifold which is simply connected (in dimension 2, all
simply connected compact complex manifolds are Kaehler).
The natural projection
induces a holomorphic map from the corresponding Calabi–Eckmann manifold M to
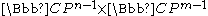. The fiber of this map is an elliptic curve T, obtained as a quotient of 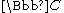by the lattice 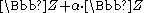. This makes M into a principalPrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
T-bundle.
Calabi and Eckmann discovered these manifolds in 1953.