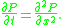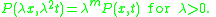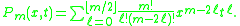Caloric polynomial
Encyclopedia
In differential equations, the mth-degree caloric polynomial (or heat polynomial) is a "parabolically m-homogeneous" polynomial Pm(x, t) that satisfies the heat equation
"Parabolically m-homogeneous" means
The polynomial is given by
It is unique up to
a factor.
With t = −1, this polynomial reduces to the mth-degree Hermite polynomial in x.
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
"Parabolically m-homogeneous" means
The polynomial is given by
It is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a factor.
With t = −1, this polynomial reduces to the mth-degree Hermite polynomial in x.