Capacitated minimum spanning tree
Encyclopedia
Capacitated minimum spanning tree is a minimal cost spanning tree
of a graph that has a designated root node
and satisfies the capacity constraint 
. The capacity constraint ensures that all subtrees (maximal subgraphs connected to the root by a single edge) incident on the root node 
have no more than 
nodes. If the tree nodes have weights, then the capacity constraint may be interpreted as follows: the sum of weights in any subtree should be no greater than 
. The edges connecting the subgraphs to the root node are called gates. To find the optimal solution, one has to go through all the possible spanning tree configurations for a given graph and pick the one with the lowest cost; such search requires an exponential number of computations.
, 
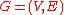with a root 
. Let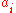 
be all other nodes in 
. Let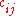 
be the edge cost between vertices 
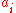and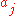 
which form a cost matrix 
.
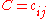Initially, all nodes are connected to the root
(star graph) and the network's cost is 
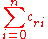; each of these edges is a gate. At each iteration, we seek the closest neighbor 
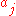for every node in 
and evaluate the tradeoff function: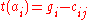 
. We look for the greatest 
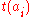among the positive tradeoffs and, if the resulting subtree does not violate the capacity constraints, remove the gate 
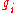connecting the 
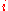-th subtree to 
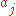by an edge 
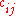. We repeat the iterations until we can not make any further improvements to the tree.
Esau-Williams heuristics for computing a suboptimal CMST:
function CMST(c,C,r):
T = {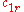
, 
, ..., 
}
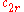while have changes:
for each node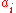
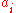= closest node in a different subtree
= 
- 
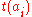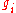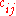
t_max = max(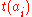
)
k = i such that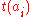
= t_max
if ( cost(i) + cost(j) <= c)
T = T -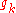
T = T union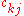
return T
It is easy to see that EW finds a solution in polynomial time.
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
of a graph that has a designated root node
and satisfies the capacity constraint . The capacity constraint ensures that all subtrees (maximal subgraphs connected to the root by a single edge) incident on the root node have no more than nodes. If the tree nodes have weights, then the capacity constraint may be interpreted as follows: the sum of weights in any subtree should be no greater than . The edges connecting the subgraphs to the root node are called gates. To find the optimal solution, one has to go through all the possible spanning tree configurations for a given graph and pick the one with the lowest cost; such search requires an exponential number of computations.Algorithms
Suppose we have a graph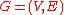, with a root . Let 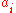be all other nodes in . Let 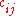be the edge cost between vertices 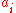and 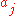which form a cost matrix 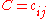.Esau-Williams heuristic
Esau-Williams heuristic finds suboptimal CMST that are very close to the exact solutions, but on average EW produces better results than many other heuristics.Initially, all nodes are connected to the root
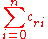(star graph) and the network's cost is ; each of these edges is a gate. At each iteration, we seek the closest neighbor 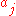for every node in and evaluate the tradeoff function: 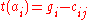. We look for the greatest 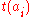among the positive tradeoffs and, if the resulting subtree does not violate the capacity constraints, remove the gate 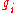connecting the 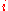-th subtree to 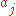by an edge 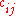. We repeat the iterations until we can not make any further improvements to the tree.Esau-Williams heuristics for computing a suboptimal CMST:
function CMST(c,C,r):
T = {
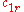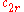, , ..., }while have changes:
for each node
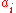
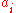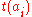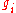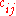
= closest node in a different subtree = - t_max = max(
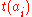)k = i such that
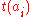= t_maxif ( cost(i) + cost(j) <= c)
T = T -
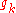
T = T union
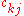
return T
It is easy to see that EW finds a solution in polynomial time.