
Carathéodory-Jacobi-Lie theorem
Encyclopedia
The Carathéodory
–Jacobi
–Lie
theorem is a theorem
in symplectic geometry which generalizes Darboux's theorem
.
with symplectic form ω. For p ∈ M and r ≤ n, let f1, f2, ..., fr be smooth function
s defined on an open neighborhood V of p whose differential
s are linearly independent at each point, or equivalently
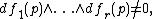
where {fi, fj} = 0. (In other words they are pairwise in involution.) Here {–,–} is the Poisson bracket
. Then there are functions fr+1, ..., fn, g1, g2, ..., gn defined on an open neighborhood U ⊂ V of p such that (fi, gi) is a symplectic chart of M, i.e., ω is expressed on U as
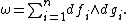
as where M is a symplectic manifold with symplectic form
where M is a symplectic manifold with symplectic form 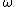 and H is the Hamiltonian function
and H is the Hamiltonian function
, around every point where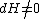 there is a chart such that one of its coordinates is H.
there is a chart such that one of its coordinates is H.
Constantin Carathéodory
Constantin Carathéodory was a Greek mathematician. He made significant contributions to the theory of functions of a real variable, the calculus of variations, and measure theory...
–Jacobi
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
–Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
theorem is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in symplectic geometry which generalizes Darboux's theorem
Darboux's theorem
Darboux's theorem is a theorem in the mathematical field of differential geometry and more specifically differential forms, partially generalizing the Frobenius integration theorem. It is a foundational result in several fields, the chief among them being symplectic geometry...
.
Statement
Let M be a 2n-dimensional symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
with symplectic form ω. For p ∈ M and r ≤ n, let f1, f2, ..., fr be smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s defined on an open neighborhood V of p whose differential
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s are linearly independent at each point, or equivalently
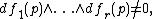
where {fi, fj} = 0. (In other words they are pairwise in involution.) Here {–,–} is the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
. Then there are functions fr+1, ..., fn, g1, g2, ..., gn defined on an open neighborhood U ⊂ V of p such that (fi, gi) is a symplectic chart of M, i.e., ω is expressed on U as
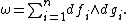
Applications
As a direct application we have the following. Given a Hamiltonian systemHamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
as
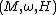 where M is a symplectic manifold with symplectic form
where M is a symplectic manifold with symplectic form 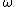 and H is the Hamiltonian function
and H is the Hamiltonian functionHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, around every point where
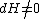 there is a chart such that one of its coordinates is H.
there is a chart such that one of its coordinates is H.

