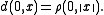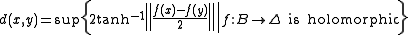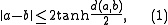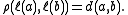Carathéodory metric
Encyclopedia
In mathematics
, the Carathéodory metric is a metric
defined on the open
unit ball of a complex
Banach space
that has many similar properties to the Poincaré metric
of hyperbolic geometry
. It is named after the Greek
mathematician
Constantin Carathéodory
.
C, thought of as the Poincaré disc model for 2-dimensional real/1-dimensional complex hyperbolic geometry. Let the Poincaré metric ρ on Δ be given by

(thus fixing the curvature
to be −4). Then the Carathéodory metric d on B is defined by
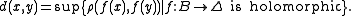
What it means for a function on a Banach space to be holomorphic is defined in the article on Infinite dimensional holomorphy.
s to the ball B. Let x be a point of B and let v be a tangent vector to B at x; since B is the open unit ball in the vector space X, the tangent space TxB can be identified with X in a natural way, and v can be thought of as an element of X. Then the Carathéodory length of v at x, denoted α(x, v), is defined by
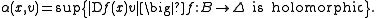
One can show that α(x, v) ≥ ||v||, with equality when x = 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Carathéodory metric is a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
defined on the open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
unit ball of a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
that has many similar properties to the Poincaré metric
Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. It is named after the Greek
Greece
Greece , officially the Hellenic Republic , and historically Hellas or the Republic of Greece in English, is a country in southeastern Europe....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Constantin Carathéodory
Constantin Carathéodory
Constantin Carathéodory was a Greek mathematician. He made significant contributions to the theory of functions of a real variable, the calculus of variations, and measure theory...
.
Definition
Let (X, || ||) be a complex Banach space and let B be the open unit ball in X. Let Δ denote the open unit disc in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C, thought of as the Poincaré disc model for 2-dimensional real/1-dimensional complex hyperbolic geometry. Let the Poincaré metric ρ on Δ be given by

(thus fixing the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
to be −4). Then the Carathéodory metric d on B is defined by
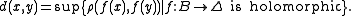
What it means for a function on a Banach space to be holomorphic is defined in the article on Infinite dimensional holomorphy.
Properties
- For any point x in B,
- d can also be given by the following formula, which Carathéodory attributed to Erhard SchmidtErhard SchmidtErhard Schmidt was a German mathematician whose work significantly influenced the direction of mathematics in the twentieth century. He was born in Tartu, Governorate of Livonia . His advisor was David Hilbert and he was awarded his doctorate from Georg-August University of Göttingen in 1905...
:
- For all a and b in B,
- with equality if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
either a = b or there exists a bounded linear functional ℓ ∈ X∗ such that ||ℓ|| = 1, ℓ(a + b) = 0 and
- Moreover, any ℓ satisfying these three conditions has |ℓ(a − b)| = ||a − b||.
- Also, there is equality in (1) if ||a|| = ||b|| and ||a − b|| = ||a|| + ||b||. One way to do this is to take b = −a.
- If there exists a unit vector u in X that is not an extreme pointExtreme pointIn mathematics, an extreme point of a convex set S in a real vector space is a point in S which does not lie in any open line segment joining two points of S...
of the closed unit ball in X, then there exist points a and b in B such that there is equality in (1) but b ≠ ±a.
Carathéodory length of a tangent vector
There is an associated notion of Carathéodory length for tangent vectorTangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s to the ball B. Let x be a point of B and let v be a tangent vector to B at x; since B is the open unit ball in the vector space X, the tangent space TxB can be identified with X in a natural way, and v can be thought of as an element of X. Then the Carathéodory length of v at x, denoted α(x, v), is defined by
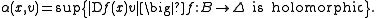
One can show that α(x, v) ≥ ||v||, with equality when x = 0.