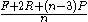The Catmull–Clark algorithm is used in computer graphics

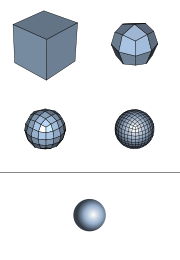
Computer graphics

Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....

 to create smooth surfaces by subdivision surface

Subdivision surface

A subdivision surface, in the field of 3D computer graphics, is a method of representing a smooth surface via the specification of a coarser piecewise linear polygon mesh...

 modeling. It was devised by Edwin Catmull

Edwin Catmull

Dr. Edwin Earl Catmull, Ph.D. is a computer scientist and current president of Walt Disney Animation Studios and Pixar Animation Studios. As a computer scientist, Catmull has contributed to many important developments in computer graphics....

 and Jim Clark

James H. Clark

James H. Clark is an American entrepreneur and computer scientist. He founded several notable Silicon Valley technology companies, including Silicon Graphics, Inc., Netscape Communications Corporation, myCFO and Healtheon...

 in 1978 as a generalization of bi-cubic uniform B-spline

B-spline

In the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...

 surfaces to arbitrary topology. In 2005, Edwin Catmull received an Academy Award for Technical Achievement

Academy Award for Technical Achievement

The Technical Achievement Award is a kind of Scientific and Technical Award given by the Academy of Motion Picture Arts and Sciences to those whose particular technical accomplishments have contributed to the progress of the motion picture industry and who are given a certificate, which describes...

 together with
Tony DeRose and Jos Stam for their invention and application of subdivision surfaces.

Recursive evaluation

Catmull–Clark surfaces are defined recursively, using the following refinement scheme:

Start with a mesh

Polygon mesh

A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...

 of an arbitrary polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

. All the vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 in this mesh shall be called original points.

• For each face, add a face point
  • Set each face point to be the centroid
    Centroid
    In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
    
     of all original points for the respective face.
• For each edge, add an edge point.
  • Set each edge point to be the average of the two neighbouring face points and its two original endpoints.
• For each face point, add an edge for every edge of the face, connecting the face point to each edge point for the face.
• For each original point P, take the average F of all n face points for faces touching P, and take the average R of all n edge midpoints for edges touching P, where each edge midpoint is the average of its two endpoint vertices. Move each original point to the point

(This is the barycenter of P, R and F with respective weights (n-3), 2 and 1. This arbitrary-looking formula was chosen by Catmull and Clark based on the aesthetic appearance of the resulting surfaces rather than on a mathematical derivation.)

The new mesh will consist only of quadrilateral

Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

s, which won't in general be planar

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

. The new mesh will generally look smoother than the old mesh.

Repeated subdivision results in smoother meshes. It can be shown that the limit surface obtained by this refinement process is at least 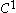at extraordinary vertices and 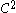everywhere else (when n indicates how many derivatives are continuous, we speak of 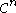continuity). After one iteration, the number of extraordinary points on the surface remains constant.

Exact evaluation

The limit surface of Catmull–Clark subdivision surfaces can also be evaluated directly, without any recursive refinement. This can be accomplished by means of the technique of Jos Stam

Jos Stam

Jos Stam is a researcher in the field of computer graphics, focusing on subdivision surfaces, rendering algorithms and the simulation of natural physical phenomena.-Education and career:...

 . This method reformulates the recursive refinement process into a matrix exponential

Matrix exponential

In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....

 problem, which can be solved directly by means of matrix diagonalization.

See also

• Conway polyhedron notation
  Conway polyhedron notation
  Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...
  
  - A set of related topological polyhedron and polygonal mesh operators.