
Cauchy formula for repeated integration
Encyclopedia
The Cauchy formula for repeated integration, named after Augustin Louis Cauchy
, allows one to compress n antidifferentiations of a function into a single integral (cf. Cauchy's formula).
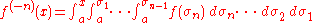 ,
,
is given by single integration
 .
.
A proof is given by induction
. Since ƒ is continuous, the base case is given by noting that
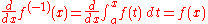
and that
 .
.
Now, suppose this is true for n; to prove it for n+1, we apply the chain rule. Consider the function
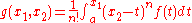 ;
;
then we have
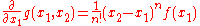
and, applying differentiation under the integral sign, we have that
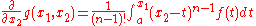 .
.
Thus,
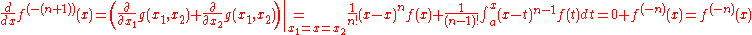 .
.
Furthermore,
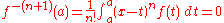 .
.
Hence, ƒ(-n) is an nth antiderivative of ƒ, and ƒ(-k)(a)=0 for all k from 1 to n, showing that ƒ(-n)(x) is equal to the original repeated integral.
, this formula can be used to construct a notion of differintegral, allowing one to differentiate or integrate a fractional number of times. Integrating a fractional number of times with this formula is straightforward; one can use fractional n by interpreting (n-1)! as Γ(n) (see Gamma function
).
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
, allows one to compress n antidifferentiations of a function into a single integral (cf. Cauchy's formula).
Scalar case
Let ƒ be a continuous function on the real line. Then the nth repeated integral of ƒ based at a,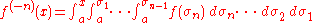 ,
,is given by single integration
 .
.A proof is given by induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. Since ƒ is continuous, the base case is given by noting that
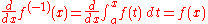
and that
 .
.Now, suppose this is true for n; to prove it for n+1, we apply the chain rule. Consider the function
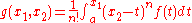 ;
;then we have
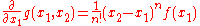
and, applying differentiation under the integral sign, we have that
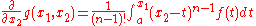 .
.Thus,
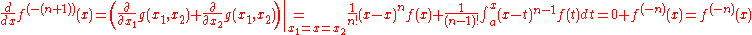 .
.Furthermore,
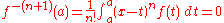 .
.Hence, ƒ(-n) is an nth antiderivative of ƒ, and ƒ(-k)(a)=0 for all k from 1 to n, showing that ƒ(-n)(x) is equal to the original repeated integral.
Applications
In fractional calculusFractional calculus
Fractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.and the integration operator J...
, this formula can be used to construct a notion of differintegral, allowing one to differentiate or integrate a fractional number of times. Integrating a fractional number of times with this formula is straightforward; one can use fractional n by interpreting (n-1)! as Γ(n) (see Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
).

