In mathematical analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

, the Cauchy index is an integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

 associated to a real rational function

Rational function

In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...

 over an interval

Interval

Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...

. By the Routh-Hurwitz theorem, we have the following interpretation: the Cauchy index of

r(x)=p(x)/q(x)

over the real line

Real line

In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...

 is the difference between the number of roots of f(z) located in the right half-plane and those located in the left-half plane. The complex polynomial f(z) is such that

f(iy)=q(y)+ip(y).

We must also assume that p has degree less than the degree of q.

Definition

• The Cauchy index was first defined for a pole s of the rational function r by Augustin Louis Cauchy
  Augustin Louis Cauchy
  Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
  
   in 1837 using one-sided limit
  One-sided limit
  In calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
  
  s as:
  
  • A generalization over the compact interval [a,b] is direct (when neither a nor b are poles of r(x)): it is the sum of the Cauchy indices of r for each s located in the interval. We usually denote it by .
  
  
  • We can then generalize to intervals of type since the number of poles of r is a finite number (by taking the limit of the Cauchy index over [a,b] for a and b going to infinity).
  
  

  Examples

  
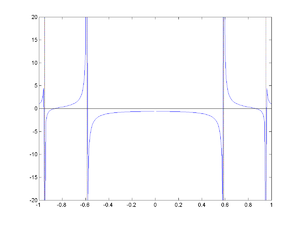
  • Consider the rational function:
  
  We recognize in p(x) and q(x) respectively the Chebyshev polynomials
  Chebyshev polynomials
  In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
  
   of degree 3 and 5. Therefore r(x) has poles , , , and , i.e. for . We can see on the picture that and . For the pole in zero, we have since the left and right limits are equal (which is because p(x) also has a root in zero).
  We conclude that since q(x) has only 5 roots, all in [-1,1]. We cannot use here the Routh-Hurwitz theorem as each complex polynomial with f(iy)=q(y)+ip(y) has a zero on the imaginary line
  Imaginary number
  An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
  
  (namely at the origin).
  The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.