Cauchy momentum equation
Encyclopedia
The Cauchy momentum equation is a vector partial differential equation
put forth by Cauchy that describes the non-relativistic momentum transport in any continuum:
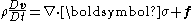
or, with the derivative
expanded out,
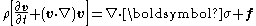
where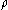
is the density
of the continuum,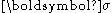
is the stress tensor
, and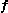
contains all of the body force
s (normally just gravity).
is the velocity vector field, which depends on time and space.
The stress tensor is sometimes split into pressure and the deviatoric stress tensor:
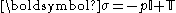
where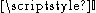
is the 
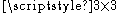identity matrix
and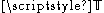
the deviatoric stress tensor. The divergence of the stress tensor can be written as
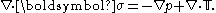
All non-relativistic momentum conservation equations, such as the Navier–Stokes equation, can be derived by beginning with the Cauchy momentum equation and specifying the stress tensor through a constitutive relation.
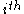component) to a control volume
in the continuum being modeled gives:
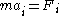
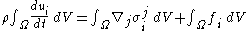
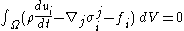
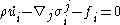
where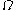
represents the control volume. Since this equation must hold for any control volume, it must be true that the integrand is zero, from this the Cauchy momentum equation follows. The main challenge in deriving this equation is establishing that the derivative of the stress tensor is one of the forces that constitutes 
.
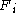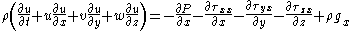
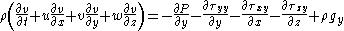
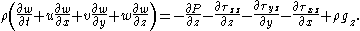
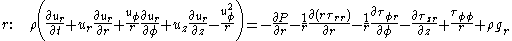
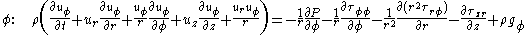
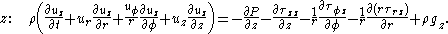
By expressing the shear stress in terms of viscosity
and fluid velocity
, and assuming constant density and viscosity, the Cauchy momentum equation will lead to the Navier–Stokes equations. By assuming inviscid flow
, the Navier–Stokes equations can further simpify to the Euler equations.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
put forth by Cauchy that describes the non-relativistic momentum transport in any continuum:
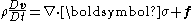
or, with the derivative
Convective derivative
The material derivative is a derivative taken along a path moving with velocity v, and is often used in fluid mechanics and classical mechanics...
expanded out,
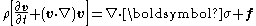
where
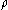is the densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of the continuum,
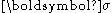is the stress tensorStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
, and
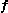contains all of the body forceBody force
A body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
s (normally just gravity).
is the velocity vector field, which depends on time and space.The stress tensor is sometimes split into pressure and the deviatoric stress tensor:
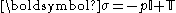
where
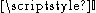is the 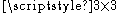identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and
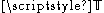the deviatoric stress tensor. The divergence of the stress tensor can be written as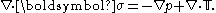All non-relativistic momentum conservation equations, such as the Navier–Stokes equation, can be derived by beginning with the Cauchy momentum equation and specifying the stress tensor through a constitutive relation.
Derivation
Applying Newton's second law (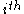 component) to a control volumeControl volume
In fluid mechanics and thermodynamics, a control volume is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a volume fixed in space or moving with constant velocity through which the fluid flows...
in the continuum being modeled gives:
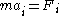
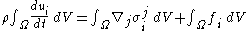
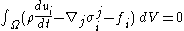
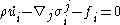
where
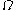represents the control volume. Since this equation must hold for any control volume, it must be true that the integrand is zero, from this the Cauchy momentum equation follows. The main challenge in deriving this equation is establishing that the derivative of the stress tensor is one of the forces that constitutes 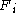.Cartesian coordinates
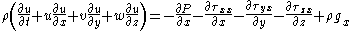
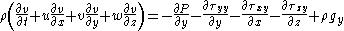
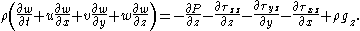
Cylindrical coordinates
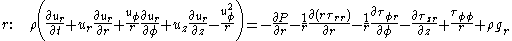
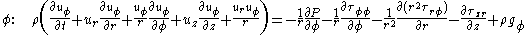
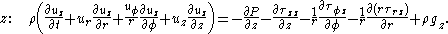
By expressing the shear stress in terms of viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
and fluid velocity
Shear velocity
Shear velocity, also called friction velocity, is a form by which a shear stress may be re-written in units of velocity. It is useful as a method in fluid mechanics to compare true velocities, such as the velocity of a flow in a stream, to a velocity that relates shear between layers of flow.Shear...
, and assuming constant density and viscosity, the Cauchy momentum equation will lead to the Navier–Stokes equations. By assuming inviscid flow
Inviscid flow
In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow....
, the Navier–Stokes equations can further simpify to the Euler equations.