Cauchy surface
Encyclopedia
Intuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future (and the past) uniquely.
More precisely, a Cauchy surface
is any subset of space-time which is intersected by every non-spacelike, inextensible curve
, i.e. any causal curve, exactly once.
A partial Cauchy surface is a hypersurface which is intersected by any causal curve at most once.
The name is for Augustin Louis Cauchy
.
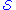is a space-like surface (i.e., a collection of points such that every pair is space-like separated), then 
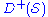is the future of 
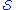, which is all the points which can be reached from 
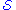while going forward in time on curves which are timelike or null. Similarly 
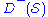, the past of 
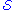, is the same thing going back in time.
When there are no closed timelike curves,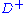
and 
are two different regions. When the time dimension closes up on itself everywhere so that it makes a circle, the future and the past of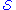 
are the same and both include 
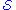. The Cauchy surface is defined pedantically in terms of intersections with inextensible curves in order to deal with this case of circular time. An inextensible curve is a curve with no ends: either it goes on forever, remaining timelike or null, or it closes in on itself to make a circle, a closed non-spacelike curve.
When there are closed timelike curves, or even when there are closed non-spacelike curves, a Cauchy surface still determines the future, but the future includes the surface itself. This means that the initial conditions obey a constraint, and the Cauchy surface is not of the same character as when the future and the past are disjoint.
If there are no closed timelike curves, then given
a partial Cauchy surface and if 
, the entire manifold
, then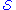
is a Cauchy surface. Any surface of constant 
in Minkowski space-time is a Cauchy surface.
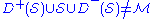then there exists a Cauchy horizon
between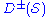
and regions of the manifold not completely determined by information on 
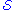. A clear physical example of a Cauchy horizon is the second horizon inside a charged or rotating black hole. The outermost horizon is an event horizon
, beyond which information cannot escape, but where the future is still determined from the conditions outside. Inside the inner horizon, the Cauchy horizon, the singularity is visible and to predict the future requires additional data about what comes out of the singularity.
Since a black hole Cauchy horizon only forms in a region where the geodesics are outgoing, in radial coordinates, in a region where the central singularity is repulsive, it is hard to imagine exactly how it forms. For this reason, Kerr and others suggest that a Cauchy horizon never forms, instead that the inner horizon is in fact a spacelike or timelike singularity.
A homogenous space-time with a Cauchy horizon is anti de Sitter space
.
More precisely, a Cauchy surface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
is any subset of space-time which is intersected by every non-spacelike, inextensible curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
, i.e. any causal curve, exactly once.
A partial Cauchy surface is a hypersurface which is intersected by any causal curve at most once.
The name is for Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
.
Discussion
If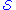 is a space-like surface (i.e., a collection of points such that every pair is space-like separated), then 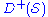is the future of 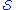, which is all the points which can be reached from 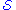while going forward in time on curves which are timelike or null. Similarly 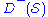, the past of 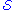, is the same thing going back in time.When there are no closed timelike curves,
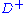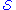and are two different regions. When the time dimension closes up on itself everywhere so that it makes a circle, the future and the past of are the same and both include 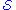. The Cauchy surface is defined pedantically in terms of intersections with inextensible curves in order to deal with this case of circular time. An inextensible curve is a curve with no ends: either it goes on forever, remaining timelike or null, or it closes in on itself to make a circle, a closed non-spacelike curve.When there are closed timelike curves, or even when there are closed non-spacelike curves, a Cauchy surface still determines the future, but the future includes the surface itself. This means that the initial conditions obey a constraint, and the Cauchy surface is not of the same character as when the future and the past are disjoint.
If there are no closed timelike curves, then given
a partial Cauchy surface and if , the entire manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, then
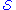is a Cauchy surface. Any surface of constant in Minkowski space-time is a Cauchy surface.Cauchy Horizon
If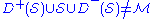 then there exists a Cauchy horizonCauchy horizon
In physics, a Cauchy horizon is a light-like boundary of the domain of validity of a Cauchy problem...
between
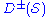and regions of the manifold not completely determined by information on 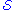. A clear physical example of a Cauchy horizon is the second horizon inside a charged or rotating black hole. The outermost horizon is an event horizonEvent horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
, beyond which information cannot escape, but where the future is still determined from the conditions outside. Inside the inner horizon, the Cauchy horizon, the singularity is visible and to predict the future requires additional data about what comes out of the singularity.
Since a black hole Cauchy horizon only forms in a region where the geodesics are outgoing, in radial coordinates, in a region where the central singularity is repulsive, it is hard to imagine exactly how it forms. For this reason, Kerr and others suggest that a Cauchy horizon never forms, instead that the inner horizon is in fact a spacelike or timelike singularity.
A homogenous space-time with a Cauchy horizon is anti de Sitter space
Anti de Sitter space
In mathematics and physics, n-dimensional anti de Sitter space, sometimes written AdS_n, is a maximally symmetric Lorentzian manifold with constant negative scalar curvature...
.