
Cayley's Ω process
Encyclopedia
In mathematics, Cayley's Ω process, introduced by , is a relatively invariant differential operator
on the general linear group
, that is used to construct invariants
of a group action
.
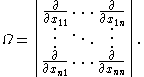
As a partial differential operator acting on functions of n2 variables xij, the omega operator is given by the determinant
used to find generators for the invariants of various classical groups acting on natural polynomial algebras.
used Cayley's Ω process in his proof of finite generation of rings of invariants of the general linear group. His use of the Ω process gives an explicit formula for the Reynolds operator
of the special linear group.
Cayley's Ω process is used to define transvectant
s.
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
on the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
, that is used to construct invariants
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
.
As a partial differential operator acting on functions of n2 variables xij, the omega operator is given by the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

Applications
Cayley's Ω process appears in Capelli's identity, whichused to find generators for the invariants of various classical groups acting on natural polynomial algebras.
used Cayley's Ω process in his proof of finite generation of rings of invariants of the general linear group. His use of the Ω process gives an explicit formula for the Reynolds operator
Reynolds operator
In fluid dynamics and invariant theory, a Reynolds operator is a mathematical operator given by averaging something over a group action, that satisfies a set of properties called Reynolds rules...
of the special linear group.
Cayley's Ω process is used to define transvectant
Transvectant
In mathematical invariant theory, a transvectant is an invariant formed from n invariants in n variables using Cayley's omega process.-Definition:...
s.

