
Reynolds operator
Encyclopedia
In fluid dynamics
and invariant theory
, a Reynolds operator is a mathematical operator given by averaging something over a group action, that satisfies a set of properties called Reynolds rules. In fluid dynamics Reynolds operators are often encountered in models of turbulent flows
, particularly the Reynolds-averaged Navier-Stokes equations
, where the average is typically taken over the fluid flow under the group of time translations. In invariant theory the average is often taken over a compact group or reductive algebraic group acting on a commutative algebra, such as a ring of polynomials. Reynolds operators were introduced into fluid dynamics by and named by .
A Reynolds operator acting on φ is sometimes denoted by R(φ), P(φ), ρ(φ), 〈φ〉, or . Reynolds operators are usually linear operators acting on some algebra of functions, satisfying the identity
and possibly some other conditions, such as commuting with various group actions.
and
Together these conditions imply that R is idempotent: R2=R. The Reynolds operator will also usually commute with some group action, and project onto the invariant elements of this group action.
The operator R is called an averaging operator if it is linear and satisfies
If R(R(φ)) = R(φ) for all φ then R is an averaging operator if and only if it is a Reynolds operator. Sometimes the R(R(φ)) = R(φ) condition is added to the definition of Reynolds operators.
 and
and  be two random variables, and
be two random variables, and  be an arbitrary constant. Then the properties satisfied by Reynolds operators, for an operator
be an arbitrary constant. Then the properties satisfied by Reynolds operators, for an operator 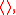 include linearity and the averaging property:
include linearity and the averaging property:
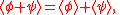

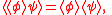 which implies
which implies 
In addition the Reynolds operator is often assumed to commute with space and time translations: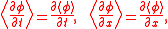

Any operator satisfying these properties is a Reynolds operator.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
and invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
, a Reynolds operator is a mathematical operator given by averaging something over a group action, that satisfies a set of properties called Reynolds rules. In fluid dynamics Reynolds operators are often encountered in models of turbulent flows
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
, particularly the Reynolds-averaged Navier-Stokes equations
Reynolds-averaged Navier-Stokes equations
The Reynolds-averaged Navier–Stokes equations are time-averagedequations of motion for fluid flow. The idea behind the equations is Reynolds decomposition, whereby an instantaneous quantity is decomposed into its time-averaged and fluctuating quantities, an idea first proposed by Osborne Reynolds...
, where the average is typically taken over the fluid flow under the group of time translations. In invariant theory the average is often taken over a compact group or reductive algebraic group acting on a commutative algebra, such as a ring of polynomials. Reynolds operators were introduced into fluid dynamics by and named by .
Definition
Reynolds operators are used in fluid dynamics, functional analysis, and invariant theory, and the notation and definitions in these areas differ slightly.A Reynolds operator acting on φ is sometimes denoted by R(φ), P(φ), ρ(φ), 〈φ〉, or . Reynolds operators are usually linear operators acting on some algebra of functions, satisfying the identity
- R(R(φ)ψ) = R(φ)R(ψ) for all φ, ψ
and possibly some other conditions, such as commuting with various group actions.
Invariant theory
In invariant theory a Reynolds operator R is usually a linear operator satisfying- R(R(φ)ψ) = R(φ)R(ψ) for all φ, ψ
and
- R(1) =1.
Together these conditions imply that R is idempotent: R2=R. The Reynolds operator will also usually commute with some group action, and project onto the invariant elements of this group action.
Functional analysis
In functional analysis a Reynolds operator is a linear operator R acting on some algebra of functions φ, satisfying the Reynolds identity- R(φψ) = R(φ)R(ψ) +R((φ−R(φ))(ψ−R(ψ))) for all φ, ψ
The operator R is called an averaging operator if it is linear and satisfies
- R(R(φ)ψ) = R(φ)R(ψ) for all φ, ψ.
If R(R(φ)) = R(φ) for all φ then R is an averaging operator if and only if it is a Reynolds operator. Sometimes the R(R(φ)) = R(φ) condition is added to the definition of Reynolds operators.
Fluid dynamics
Let and
and  be two random variables, and
be two random variables, and  be an arbitrary constant. Then the properties satisfied by Reynolds operators, for an operator
be an arbitrary constant. Then the properties satisfied by Reynolds operators, for an operator 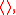 include linearity and the averaging property:
include linearity and the averaging property: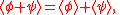

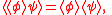 which implies
which implies 
In addition the Reynolds operator is often assumed to commute with space and time translations:
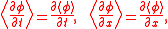

Any operator satisfying these properties is a Reynolds operator.
Examples
Reynolds operators are often given by projecting onto an invariant subspace of a group action.- The "Reynolds operator" considered by was essentially the projection of a fluid flow to the "average" fluid flow, which can be thought of as projection to time-invariant flows. Here the group action is given by the action of the group of time-translations.
- Suppose that G is a reductive algebraic group or a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
group, and V is a finite-dimensional representation of G. Then G also acts on the symmetric algebra SV of polynomials. The Reynolds operator R is the G-invariant projection from SV to the subring SVG of elements fixed by G.

