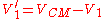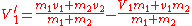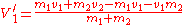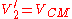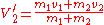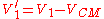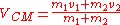Center of momentum frame
Encyclopedia
A center-of-momentum frame (zero-momentum frame, or COM frame) of a system is any inertial frame in which the center of mass
is at rest (has zero velocity). Note that the center of momentum of a system is not a location, but rather defines a particular inertial frame (a velocity and a direction). Thus "center of momentum" already means "center-of-momentum frame" and is a short form of this phrase.
A special case of the center-of-momentum frame is the center-of-mass frame: an inertial frame in which the center of mass (which is a physical point) is at the origin at all times. In all COM frames, the center of mass is at rest, but it may not necessarily be at rest at the origin of the coordinate system.
, COM frame exists for a massive system. In the COM frame the total energy of the system is the "rest energy", and this quantity (when divided by the factor c2) therefore gives the rest mass (positive invariant mass) of the system.
Systems which have energy but zero invariant mass
(such as photons moving in a single direction, or equivalently, plane
electromagnetic waves) do not have COM frames, because there is no frame which they have zero net momentum. Because of the invariance of the speed of light
, such massless systems must travel at the speed of light in any frame, and therefore always possess a net momentum-magnitude which is equal to their energy divided by the speed of light: p = E/c.
where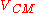
is given by:
If we take two particles, one of mass m1 moving at velocity V1 and a second of mass m2, then we can apply the following formulae:
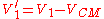
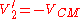
After their collision, they will have speeds:
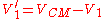
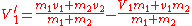
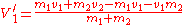
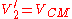
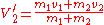
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
is at rest (has zero velocity). Note that the center of momentum of a system is not a location, but rather defines a particular inertial frame (a velocity and a direction). Thus "center of momentum" already means "center-of-momentum frame" and is a short form of this phrase.
A special case of the center-of-momentum frame is the center-of-mass frame: an inertial frame in which the center of mass (which is a physical point) is at the origin at all times. In all COM frames, the center of mass is at rest, but it may not necessarily be at rest at the origin of the coordinate system.
Properties
In the centre of momentum frame, the total linear momentum of the system is zero. Also, the total energy of the system is the minimal energy as seen from all possible inertial reference frames. In relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, COM frame exists for a massive system. In the COM frame the total energy of the system is the "rest energy", and this quantity (when divided by the factor c2) therefore gives the rest mass (positive invariant mass) of the system.
Systems which have energy but zero invariant mass
Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
(such as photons moving in a single direction, or equivalently, plane
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
electromagnetic waves) do not have COM frames, because there is no frame which they have zero net momentum. Because of the invariance of the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, such massless systems must travel at the speed of light in any frame, and therefore always possess a net momentum-magnitude which is equal to their energy divided by the speed of light: p = E/c.
Example problem
An example of the usage of this frame is given below – in a two-body elastic collision problem. The transformations applied are to take the velocity of the frame from the velocity of each particle:
where
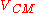is given by:
If we take two particles, one of mass m1 moving at velocity V1 and a second of mass m2, then we can apply the following formulae:
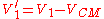
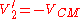
After their collision, they will have speeds: