Central limit theorem for directional statistics
Encyclopedia
In probability theory
, the central limit theorem
states conditions under which the mean of a sufficiently large number of independent
random variables, each with finite mean and variance, will be approximately normally distributed.
Directional statistics is the subdiscipline of statistics
that deals with directions (unit vectors in Rn), axes
(lines through the origin in Rn) or rotation
s in Rn. The means and variances of directional quantities are all finite, so that the central limit theorem may be applied to the particular case of directional statistics.
This article will deal only with unit vectors in 2-dimensional space (R2) but the method described can be extended to the general case.
are measured, and since they are indefinite to within a factor of 
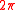, the complex definite quantity 
is used as the random variate. The probability distribution from which the sample is drawn may be characterized by its moments, which may be expressed in Cartesian and polar form:
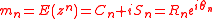
It follows that:
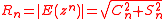
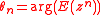
Sample moments for N trials are:
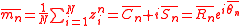
where
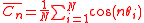
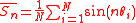
The vector [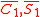
] may be used as a representation of the sample mean 
and may be taken as a 2-dimensional random variate. The bivariate central limit theorem
states that the joint probability distribution for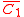
and 
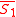in the limit of a large number of samples is given by:
where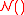
is the bivariate normal distribution and 
is the covariance matrix
for the circular distribution:
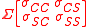
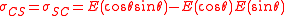
Note that the bivariate normal distribution is defined over the entire plane, while the mean is confined to be in the unit ball (on or inside the unit circle). This means that the integral of the limiting (bivariate normal) distribution over the unit ball will not be equal to unity, but rather approach unity as N approaches infinity.
It is desired to state the limiting bivariate distribution in terms of the moments of the distribution.
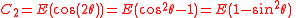
It follows that:
The covariance matrix is now expressed in terms of the moments of the circular distribution.
The central limit theorem may also be expressed in terms of the polar components of the mean. If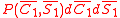
is the probability of finding the mean in area element 
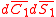, then that probability may also be written 
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
states conditions under which the mean of a sufficiently large number of independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variables, each with finite mean and variance, will be approximately normally distributed.
Directional statistics is the subdiscipline of statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
that deals with directions (unit vectors in Rn), axes
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
(lines through the origin in Rn) or rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s in Rn. The means and variances of directional quantities are all finite, so that the central limit theorem may be applied to the particular case of directional statistics.
This article will deal only with unit vectors in 2-dimensional space (R2) but the method described can be extended to the general case.
The central limit theorem
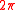A sample of angles are measured, and since they are indefinite to within a factor of , the complex definite quantity is used as the random variate. The probability distribution from which the sample is drawn may be characterized by its moments, which may be expressed in Cartesian and polar form: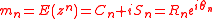It follows that:
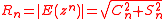
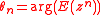
Sample moments for N trials are:
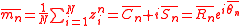
where
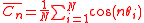
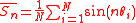
The vector [
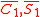] may be used as a representation of the sample mean and may be taken as a 2-dimensional random variate. The bivariate central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
states that the joint probability distribution for
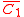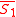and in the limit of a large number of samples is given by:where
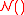is the bivariate normal distribution and is the covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
for the circular distribution:
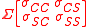
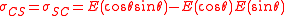
Note that the bivariate normal distribution is defined over the entire plane, while the mean is confined to be in the unit ball (on or inside the unit circle). This means that the integral of the limiting (bivariate normal) distribution over the unit ball will not be equal to unity, but rather approach unity as N approaches infinity.
It is desired to state the limiting bivariate distribution in terms of the moments of the distribution.
Covariance matrix in terms of moments
Using multiple angle trigonometric identities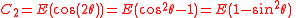It follows that:
The covariance matrix is now expressed in terms of the moments of the circular distribution.
The central limit theorem may also be expressed in terms of the polar components of the mean. If
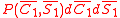is the probability of finding the mean in area element 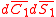, then that probability may also be written .