
Characteristic 2 type
Encyclopedia
In mathematical finite group theory, a group is said to be of characteristic 2 type or even type or of even characteristic if it resembles a group of Lie type over a field of characteristic 2.
In the classification of finite simple groups
, there is a major division between group of characteristic 2 type, where involutions resemble unipotent elements, and other groups, where involutions resemble semisimple elements.
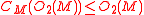 for all maximal 2-local subgroups M that contain a Sylow 2-subgroup of G.
for all maximal 2-local subgroups M that contain a Sylow 2-subgroup of G.
If this condition holds for all maximal 2-local subgroups M then G is said to be of characteristic 2 type.
use a modified version of this called even type.
In the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, there is a major division between group of characteristic 2 type, where involutions resemble unipotent elements, and other groups, where involutions resemble semisimple elements.
Definitions
A group is said to be of even characteristic if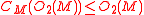 for all maximal 2-local subgroups M that contain a Sylow 2-subgroup of G.
for all maximal 2-local subgroups M that contain a Sylow 2-subgroup of G.If this condition holds for all maximal 2-local subgroups M then G is said to be of characteristic 2 type.
use a modified version of this called even type.

