Chebyshev equation
Encyclopedia
Chebyshev's equation is the second order linear differential equation
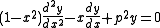
where p is a real constant. The equation is named after Russia
n mathematician Pafnuty Chebyshev
.
The solutions are obtained by power series:
where the coefficients obey the recurrence relation
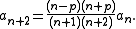
These series converge for x in
, as may be seen by applying
the ratio test to the recurrence.
The recurrence may be started with arbitrary values of a0 and a1,
leading to the two-dimensional space of solutions that arises from second order
differential equations. The standard choices are:
and
The general solution is any linear combination of these two.
When p is an integer, one or the other of the two functions has its series terminate
after a finite number of terms: F terminates if p is even, and G terminates if p is odd.
In this case, that function is a pth degree polynomial (converging
everywhere, of course), and that polynomial is proportional to the pth
Chebyshev polynomial.
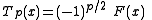if p is even
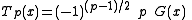if p is odd
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
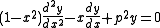
where p is a real constant. The equation is named after Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician Pafnuty Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
.
The solutions are obtained by power series:
where the coefficients obey the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
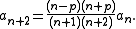
These series converge for x in
, as may be seen by applyingthe ratio test to the recurrence.
The recurrence may be started with arbitrary values of a0 and a1,
leading to the two-dimensional space of solutions that arises from second order
differential equations. The standard choices are:
- a0 = 1 ; a1 = 0, leading to the solution
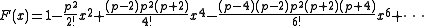
and
- a0 = 0 ; a1 = 1, leading to the solution
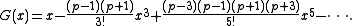
The general solution is any linear combination of these two.
When p is an integer, one or the other of the two functions has its series terminate
after a finite number of terms: F terminates if p is even, and G terminates if p is odd.
In this case, that function is a pth degree polynomial (converging
everywhere, of course), and that polynomial is proportional to the pth
Chebyshev polynomial.
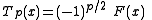if p is even 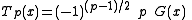if p is odd