CheiRank
Encyclopedia
The CheiRank is an eigenvector with a maximal real eigenvalue of the Google matrix
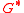constructed for a directed network with the inverted directions of links. It is similar to the PageRank
vector, which ranks the network nodes in average proportionally to a number of incoming links being the maximal eigenvector of the Google matrix
with a given initial direction of links. Due to inversion of link directions the CheiRank ranks the network nodes in average proportionally to a number of outgoing links. Since each node belongs both to CheiRank and PageRank
vectors the ranking of information flow on a directed network becomes two-dimensional.
. The PageRank
vector is the eigenvector with the maximal real eigenvalue
. It was introduce in [1] and is discussed in the article PageRank
. In a similar way the CheiRank is the eigenvector with the maximal real eigenvalue of the matrix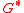
built in the same way as 
but using inverted direction of links in the initially given adjacency matrix. Both matrices 
and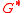 
belong to the class of Perron–Frobenius operators and according to the Perron–Frobenius theorem
the CheiRank
and PageRank 
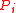eigenvectors have nonnegative components which can be interpreted as probabilities [2,3]. Thus all 
nodes 
of the network can be ordered in a decreasing probability order with ranks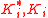 
for CheiRank and PageRank 
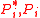respectively. In average the PageRank probability 
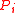is proportional to the number of ingoing links with 
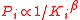[4,5,6]. For the World Wide Web (WWW) network the exponent 
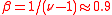where 
is the exponent for ingoing links distribution [4,5]. In a similar way the CheiRank probability is in average proportional to the number of outgoing links with
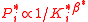with
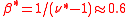where 
is the exponent for outgoing links distribution of the WWW [4,5]. The CheiRank was introduced for the procedure call network of Linux Kernel software in [6], the term itself was used in [7]. While the PageRank highlights very well known and popular nodes, the CheiRank highlights very communicative nodes. Top PageRank and CheiRank nodes have certain analogy to authorities and hubs appearing in the HITS algorithm
[9] but the HITS is query dependent while the rank probabilities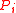
and 
classify all nodes of the network. Since each node belongs both to CheiRank and PageRank we obtain a two-dimensional ranking of network nodes.
The dependence of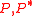
on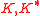 
for the network of hyperlink network of Wikipedia English articles is shown in Fig.2 from [8]. The distribution of these articles in the plane of PageRank and CheiRank is shown in Fig.3 from [8]. The difference between PageRank and CheiRank is clearly seen from the names of Wikipedia articles (2009) with highest rank. At the top of PageRank we have 1.United States, 2.United Kingdom, 3.France while for CheiRank we find 1.Portal:Contents/Outline of knowledge/Geography and places, 2.List of state leaders by year, 3.Portal:Contents/Index/Geography and places. Clearly PageRank selects first articles on a broadly known subject with a large number of ingoing links while CheiRank selects first highly communicative articles with many outgoing links. Since the articles are distributed in 2D they can be ranked in various ways corresponding to projection of 2D set on a line. The horizontal and vertical lines correspond to PageRank and CheiRank, 2DRank combines properties of CheiRank and PageRank as it is discussed in [8]. It gives top Wikipedia articles 1.India, 2.Singapore, 3.Pakistan.
The 2D ranking highlights the properties of Wikipedia articles in a new rich and fruitful manner. According to the PageRank the top 100 personalities described in Wikipedia articles have in 5 main category activities: 58 (politics), 10 (religion),17 (arts), 15 (science), 0 (sport) and thus the importance of politicians is strongly overestimated. The CheiRank gives respectively 15, 1, 52, 16, 16 while for 2DRank one finds 24, 5, 62, 7, 2.
Such type of 2D ranking can find useful applications for various complex directed networks including the WWW.
CheiRank and PageRank naturally appear for the world trade network,
or international trade
,
where they and linked with export and import flows for a given country respectively [10].
Possibilities of development of two-dimensional search engines based on PageRank and CheiRank are considered in [11].
and 
, used for determination of the related PageRank and CheiRank vectors, is given below. The directed network example with 7 nodes is shown in Fig.4. The matrix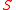 
, built with the rules described
in the article Google matrix
, is shown in Fig.5;
the related Google matrix is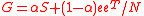
and the PageRank vector is the right eigenvector of
with the unit eigenvalue (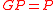
). In a similar way, to determine the CheiRank eigenvector all directions of links in Fig.4 are inverted,
then the matrix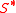
is built,
according to the same rules applied for the network with inverted link
directions, as shown in Fig.6. The related Google matrix is
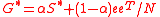and the CheiRank vector
is the right eigenvector of
with the unit eigenvalue (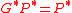
). Here 
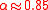is the damping factor taken at its usual value.
Google matrix
A Google matrix is a particular stochastic matrix that is used by Google's PageRank algorithm. The matrix represents a graph with edges representing links between pages....
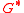constructed for a directed network with the inverted directions of links. It is similar to the PageRankPageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
vector, which ranks the network nodes in average proportionally to a number of incoming links being the maximal eigenvector of the Google matrix
Google matrix
A Google matrix is a particular stochastic matrix that is used by Google's PageRank algorithm. The matrix represents a graph with edges representing links between pages....
with a given initial direction of links. Due to inversion of link directions the CheiRank ranks the network nodes in average proportionally to a number of outgoing links. Since each node belongs both to CheiRank and PageRankPageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
vectors the ranking of information flow on a directed network becomes two-dimensional.
Definition
For a given directed network the Google matrix is constructed in the way described in the article Google matrixGoogle matrix
A Google matrix is a particular stochastic matrix that is used by Google's PageRank algorithm. The matrix represents a graph with edges representing links between pages....
. The PageRank
PageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
vector is the eigenvector with the maximal real eigenvalue
. It was introduce in [1] and is discussed in the article PageRankPageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
. In a similar way the CheiRank is the eigenvector with the maximal real eigenvalue of the matrix
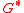built in the same way as but using inverted direction of links in the initially given adjacency matrix. Both matrices and 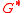belong to the class of Perron–Frobenius operators and according to the Perron–Frobenius theoremPerron–Frobenius theorem
In linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
the CheiRank
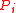and PageRank eigenvectors have nonnegative components which can be interpreted as probabilities [2,3]. Thus all nodes of the network can be ordered in a decreasing probability order with ranks 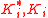for CheiRank and PageRank 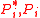respectively. In average the PageRank probability 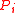is proportional to the number of ingoing links with 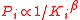[4,5,6]. For the World Wide Web (WWW) network the exponent 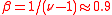where is the exponent for ingoing links distribution [4,5]. In a similar way the CheiRank probability is in average proportional to the number of outgoing links wi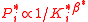th with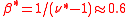 where is the exponent for outgoing links distribution of the WWW [4,5]. The CheiRank was introduced for the procedure call network of Linux Kernel software in [6], the term itself was used in [7]. While the PageRank highlights very well known and popular nodes, the CheiRank highlights very communicative nodes. Top PageRank and CheiRank nodes have certain analogy to authorities and hubs appearing in the HITS algorithmHITS algorithm
Hyperlink-Induced Topic Search is a link analysis algorithm that rates Web pages, developed by Jon Kleinberg. It was a precursor to PageRank...
[9] but the HITS is query dependent while the rank probabilities
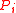and classify all nodes of the network. Since each node belongs both to CheiRank and PageRank we obtain a two-dimensional ranking of network nodes.Examples
An example of nodes distribution in the plane of PageRank and CheiRank is shown in Fig.1 for the procedure call network of Linux Kernel software taken from [7].The dependence of
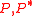on 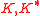for the network of hyperlink network of Wikipedia English articles is shown in Fig.2 from [8]. The distribution of these articles in the plane of PageRank and CheiRank is shown in Fig.3 from [8]. The difference between PageRank and CheiRank is clearly seen from the names of Wikipedia articles (2009) with highest rank. At the top of PageRank we have 1.United States, 2.United Kingdom, 3.France while for CheiRank we find 1.Portal:Contents/Outline of knowledge/Geography and places, 2.List of state leaders by year, 3.Portal:Contents/Index/Geography and places. Clearly PageRank selects first articles on a broadly known subject with a large number of ingoing links while CheiRank selects first highly communicative articles with many outgoing links. Since the articles are distributed in 2D they can be ranked in various ways corresponding to projection of 2D set on a line. The horizontal and vertical lines correspond to PageRank and CheiRank, 2DRank combines properties of CheiRank and PageRank as it is discussed in [8]. It gives top Wikipedia articles 1.India, 2.Singapore, 3.Pakistan.The 2D ranking highlights the properties of Wikipedia articles in a new rich and fruitful manner. According to the PageRank the top 100 personalities described in Wikipedia articles have in 5 main category activities: 58 (politics), 10 (religion),17 (arts), 15 (science), 0 (sport) and thus the importance of politicians is strongly overestimated. The CheiRank gives respectively 15, 1, 52, 16, 16 while for 2DRank one finds 24, 5, 62, 7, 2.
Such type of 2D ranking can find useful applications for various complex directed networks including the WWW.
CheiRank and PageRank naturally appear for the world trade network,
or international trade
International trade
International trade is the exchange of capital, goods, and services across international borders or territories. In most countries, such trade represents a significant share of gross domestic product...
,
where they and linked with export and import flows for a given country respectively [10].
Possibilities of development of two-dimensional search engines based on PageRank and CheiRank are considered in [11].
Simple network example
A simple example of the construction of the Google matrices and , used for determination of the related PageRank and CheiRank vectors, is given below. The directed network example with 7 nodes is shown in Fig.4. The matrix 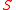, built with the rules describedin the article Google matrix
Google matrix
A Google matrix is a particular stochastic matrix that is used by Google's PageRank algorithm. The matrix represents a graph with edges representing links between pages....
, is shown in Fig.5;
the related Google matrix is
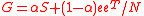
and the PageRank vector is the right eigenvector of
with the unit eigenvalue (
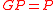). In a similar way, to determine the CheiRank eigenvector all directions of links in Fig.4 are inverted,then the matrix
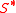is built,according to the same rules applied for the network with inverted link
directions, as shown in Fig.6. The related Google matrix is
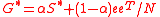and the CheiRank vectoris the right eigenvector of
with the unit eigenvalue (
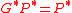). Here 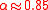is the damping factor taken at its usual value.See also
- PageRankPageRankPageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
, HITS algorithmHITS algorithmHyperlink-Induced Topic Search is a link analysis algorithm that rates Web pages, developed by Jon Kleinberg. It was a precursor to PageRank...
, Google matrixGoogle matrixA Google matrix is a particular stochastic matrix that is used by Google's PageRank algorithm. The matrix represents a graph with edges representing links between pages.... - Markov chains, Transfer operatorTransfer operatorIn mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
, Perron–Frobenius theoremPerron–Frobenius theoremIn linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of... - Information retrievalInformation retrievalInformation retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
- Web search engines