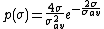Chi-square target models
Encyclopedia
Swerling models were introduced by Peter Swerling
and are used to describe the statistical properties of the radar cross-section of complex objects.
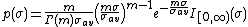
where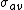 refers to the mean
refers to the mean
value of . This is not always easy to determine, as certain objects may be viewed the most frequently from a limited range of angles. For instance, a sea-based radar system is most likely to view a ship from the side, the front, and the back, but never the top or the bottom.
. This is not always easy to determine, as certain objects may be viewed the most frequently from a limited range of angles. For instance, a sea-based radar system is most likely to view a ship from the side, the front, and the back, but never the top or the bottom. 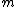 is the degree of freedom
is the degree of freedom
divided by 2. The degree of freedom used in the chi-squared probability density function is a positive number related to the target model. Values of between 0.3 and 2 have been found to closely approximate certain simple shapes, such as cylinders or cylinders with fins.
between 0.3 and 2 have been found to closely approximate certain simple shapes, such as cylinders or cylinders with fins.
Since the ratio of the standard deviation to the mean value of the chi-squared pdf is equal to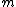 -1/2, larger values of
-1/2, larger values of  will result in less fluctuations. If
will result in less fluctuations. If 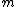 equals infinity, the target's RCS is non-fluctuating.
equals infinity, the target's RCS is non-fluctuating.
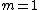 ). This applies to a target that is made up of many independent scatterers of roughly equal areas. As little as half a dozen scattering surfaces can produce this distribution. Swerling I describes a target whose radar cross-section is constant throughout a single scan, but varies independently from scan to scan. In this case, the pdf reduces to
). This applies to a target that is made up of many independent scatterers of roughly equal areas. As little as half a dozen scattering surfaces can produce this distribution. Swerling I describes a target whose radar cross-section is constant throughout a single scan, but varies independently from scan to scan. In this case, the pdf reduces to
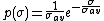
Swerling I has been shown to be a good approximation when determining the RCS of objects in aviation.
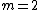 ). This PDF approximates an object with one large scattering surface with several other small scattering surfaces. The RCS is constant through a single scan just as in Swerling I. The pdf becomes
). This PDF approximates an object with one large scattering surface with several other small scattering surfaces. The RCS is constant through a single scan just as in Swerling I. The pdf becomes
Peter Swerling
Peter Swerling was one of the most influential radar theoreticians in the second half of the 20th century. He is best known for the class of statistically "fluctuating target" scattering models he developed at the RAND Corporation in the early 1950s to characterize the performance of pulsed radar...
and are used to describe the statistical properties of the radar cross-section of complex objects.
General Target Model
Swerling target models give the RCS of a given object using a distribution in the location-scale family of the chi-squared distribution.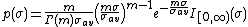
where
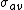 refers to the mean
refers to the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
value of
 . This is not always easy to determine, as certain objects may be viewed the most frequently from a limited range of angles. For instance, a sea-based radar system is most likely to view a ship from the side, the front, and the back, but never the top or the bottom.
. This is not always easy to determine, as certain objects may be viewed the most frequently from a limited range of angles. For instance, a sea-based radar system is most likely to view a ship from the side, the front, and the back, but never the top or the bottom. 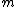 is the degree of freedom
is the degree of freedomDegrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
divided by 2. The degree of freedom used in the chi-squared probability density function is a positive number related to the target model. Values of
 between 0.3 and 2 have been found to closely approximate certain simple shapes, such as cylinders or cylinders with fins.
between 0.3 and 2 have been found to closely approximate certain simple shapes, such as cylinders or cylinders with fins.Since the ratio of the standard deviation to the mean value of the chi-squared pdf is equal to
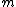 -1/2, larger values of
-1/2, larger values of  will result in less fluctuations. If
will result in less fluctuations. If 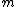 equals infinity, the target's RCS is non-fluctuating.
equals infinity, the target's RCS is non-fluctuating.Swerling Target Models
Swerling target models are special cases of the Chi-Squared target models with specific degrees of freedom. There are five different Swerling models, numbered I through V:Swerling I
A model where the RCS varies according to a Chi-squared probability density function with two degrees of freedom (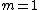 ). This applies to a target that is made up of many independent scatterers of roughly equal areas. As little as half a dozen scattering surfaces can produce this distribution. Swerling I describes a target whose radar cross-section is constant throughout a single scan, but varies independently from scan to scan. In this case, the pdf reduces to
). This applies to a target that is made up of many independent scatterers of roughly equal areas. As little as half a dozen scattering surfaces can produce this distribution. Swerling I describes a target whose radar cross-section is constant throughout a single scan, but varies independently from scan to scan. In this case, the pdf reduces to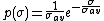
Swerling I has been shown to be a good approximation when determining the RCS of objects in aviation.
Swerling II
Similar to Swerling I, except the RCS values returned are independent from pulse to pulse, instead of scan to scan.Swerling III
A model where the RCS varies according to a Chi-squared probability density function with four degrees of freedom (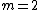 ). This PDF approximates an object with one large scattering surface with several other small scattering surfaces. The RCS is constant through a single scan just as in Swerling I. The pdf becomes
). This PDF approximates an object with one large scattering surface with several other small scattering surfaces. The RCS is constant through a single scan just as in Swerling I. The pdf becomes