Regular chiliagon
A whole regular chiliagon is not visually discernible from a circle. The lower section is a portion of a regular chiliagon, 200 times larger than the smaller one, with the vertices highlighted.
Edge Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... s and vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...	1000
Schläfli symbol	{1000}
Coxeter–Dynkin diagram
Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...	Dihedral (D1000)
Internal angle Internal angle In geometry, an interior angle is an angle formed by two sides of a polygon that share an endpoint. For a simple, convex or concave polygon, this angle will be an angle on the 'inner side' of the polygon... (degree Degree (angle) A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians... s)	179.64°
Properties	convex Convex polygon In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set... , cyclic, equilateral Equilateral In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths... , isogonal, isotoxal

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a chiliagon is a polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

 with 1000 sides.

Properties

The measure of each internal angle

Internal angle

In geometry, an interior angle is an angle formed by two sides of a polygon that share an endpoint. For a simple, convex or concave polygon, this angle will be an angle on the 'inner side' of the polygon...

 in a regular chiliagon is 179.64°. The area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

 of a regular

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

 chiliagon with sides of length a is given by

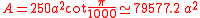
This result differs from the area of its circumscribed circle

Circumscribed circle

In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....

 by less than 0.0004%.

Because 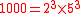, it is not a product of distinct Fermat primes and a power of two, thus the regular chiliagon it is not a constructible polygon

Constructible polygon

In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....

.

Philosophical construction

René Descartes

René Descartes

René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...

 uses the chiliagon as an example in his Sixth meditation to demonstrate the difference between pure intellection and imagination. He says that, when one thinks of a chiliagon, he "does not imagine the thousand sides or see them as if they were present" before him -- as he does when one imagines a triangle, for example. The imagination constructs a "confused representation," which is no different from that which it constructs of a myriagon. However, he does clearly understand what a chiliagon is, just as he understands what a triangle is, and he is able to distinguish it from a myriagon. Therefore, the intellect is not dependent on imagination, Descartes claims, as it is able to entertain clear and distinct ideas when imagination is unable to.