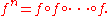Church encoding
Encyclopedia
In mathematics
, Church encoding is a means of embedding data and operators into the lambda calculus
, the most familiar form being the Church numerals, a representation of the natural numbers using lambda notation. The method is named for Alonzo Church
, who first encoded data in the lambda calculus this way.
Terms that are usually considered primitive in other notations (such as integers, booleans, pairs, lists, and tagged unions) are mapped to higher-order function
s under Church encoding; the Church-Turing thesis asserts that any computable operator (and its operands) can be represented under Church encoding.
Many students of mathematics are familiar with Gödel numbering members of a set; Church encoding is an equivalent operation defined on lambda abstractions instead of natural numbers.
s under Church encoding. The higher-order function
that represents natural number
is a function that maps any function 
to its n-fold composition
. In simpler terms, the "value" of the numeral is equivalent to the number of times the function encapsulates its argument.
Church numerals 0, 1, 2, ..., are defined as follows in the lambda calculus
:
That is, the natural number
is represented by the Church numeral n, which has the property that for any lambda-terms
The addition function plus(m,n)=m+n uses the identity
.
The successor function succ(n)=n+1 is β-equivalent to (plus 1).
The multiplication function mult(m,n)=m*n uses the identity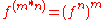
.
The exponentiation function exp(m,n)=m^n is straightforward using the multiplication function defined above.
The predecessor function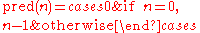
works by generating an 
-fold composition of functions that each apply their argument
The subtraction function can be written based on the predecessor function.
The zero predicate can be written as:
Now:
T and F can be arbitrary terms, for example the two Booleans as described elsewhere in this article.
) convert between nonnegative integers and their corresponding church numerals. Implementations of these conversions in other languages are similar.
In Haskell, the
and Pico. The boolean values
are represented as functions of two values that evaluate to one or the other of their arguments.
Formal definition in lambda calculus
:
Note that this definition allows predicates (i.e. functions returning logical values) to directly act as if-clauses, e.g. if predicate is a unary predicate,
evaluates to then-clause if predicate x evaluates to true, and to else-clause if predicate x evaluates to false.
Functions of boolean arithmetic can be derived for Church booleans:
Some examples:
(two-tuple) type. The pair is represented as a function that takes a function argument. When given its argument it will apply the argument to the two components of the pair.
Formal definition in lambda calculus
:
An example:
) lists of varying length must define a constructor for creating an empty list (nil), an operation testing whether or not a list is empty (isnil), an operation to prepend a given value to a (possibly empty) list (cons), and two operations to determine the first element and the list of the remaining elements of a nonempty list (head and tail).
. Using this idea the basic list operations can be defined like this:
The second component of the pair encoding nil is never used provided that head and tail are only applied to nonempty lists.
Alternatively, one can define
where the last definition is a special case of the general
. For example, a list of three elements x, y and z can be encoded by a higher-order function which when applied to a combinator c and a value n returns c x (c y (c z n))).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Church encoding is a means of embedding data and operators into the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, the most familiar form being the Church numerals, a representation of the natural numbers using lambda notation. The method is named for Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
, who first encoded data in the lambda calculus this way.
Terms that are usually considered primitive in other notations (such as integers, booleans, pairs, lists, and tagged unions) are mapped to higher-order function
Higher-order function
In mathematics and computer science, higher-order functions, functional forms, or functionals are functions which do at least one of the following:*take one or more functions as an input*output a function...
s under Church encoding; the Church-Turing thesis asserts that any computable operator (and its operands) can be represented under Church encoding.
Many students of mathematics are familiar with Gödel numbering members of a set; Church encoding is an equivalent operation defined on lambda abstractions instead of natural numbers.
Church numerals
Church numerals are the representations of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s under Church encoding. The higher-order function
Higher-order function
In mathematics and computer science, higher-order functions, functional forms, or functionals are functions which do at least one of the following:*take one or more functions as an input*output a function...
that represents natural number
is a function that maps any function to its n-fold compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. In simpler terms, the "value" of the numeral is equivalent to the number of times the function encapsulates its argument.
Definition
All Church numerals are functions that take two parameters. Here f is the successor function and x represents 0.Church numerals 0, 1, 2, ..., are defined as follows in the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
:
- 0 ≡
λf.λx. x - 1 ≡
λf.λx. f x - 2 ≡
λf.λx. f (f x) - 3 ≡
λf.λx. f (f (f x)) - ...
- n ≡
λf.λx. fn x - ...
That is, the natural number
is represented by the Church numeral n, which has the property that for any lambda-terms F and X,- n
F X=βFn X
Computation with Church numerals
In the lambda calculus, numeric functions are representable by corresponding functions on Church numerals. These functions can be implemented in most functional programming languages (subject to type constraints) by direct translation of lambda terms.The addition function plus(m,n)=m+n uses the identity
.- plus ≡
λm.λn.λf.λx. m f (n f x)
The successor function succ(n)=n+1 is β-equivalent to (plus 1).
- succ ≡
λn.λf.λx. f (n f x)
The multiplication function mult(m,n)=m*n uses the identity
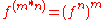.- mult ≡
λm.λn.λf.λx. m (n f) x
The exponentiation function exp(m,n)=m^n is straightforward using the multiplication function defined above.
- exp ≡
λm.λn. n (mult m) 1
The predecessor function
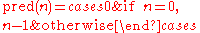works by generating an -fold composition of functions that each apply their argument g to f; the base case discards its copy of f and returns x.- pred ≡
λn.λf.λx. n (λg.λh. h (g f)) (λu. x) (λu. u)
The subtraction function can be written based on the predecessor function.
- sub ≡
λm.λn. (n pred) m
The zero predicate can be written as:
- zero? ≡
λn. n (λx.F) T
Now:
- zero? n =β T if n =β 0.
- zero? n =β F if n ≠β 0, provided n is a Church numeral and where ≠β is the negation of =β restricted to reducible lambda terms.
T and F can be arbitrary terms, for example the two Booleans as described elsewhere in this article.
Translation with other representations
Most real-world languages have support for machine-native integers; the church and unchurch functions (given here in HaskellHaskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
) convert between nonnegative integers and their corresponding church numerals. Implementations of these conversions in other languages are similar.
type Church a = (a -> a) -> (a -> a)
church :: Integer -> Church Integer
church 0 = \f -> \x -> x
church n = \f -> \x -> f (church (n-1) f x)
unchurch :: Church Integer -> Integer
unchurch n = n (\x -> x + 1) 0
In Haskell, the
\ corresponds to the λ of Lambda calculus.Church booleans
Church booleans are the Church encoding of the boolean values true and false. Some programming languages use these as an implementation model for boolean arithmetic; examples are SmalltalkSmalltalk
Smalltalk is an object-oriented, dynamically typed, reflective programming language. Smalltalk was created as the language to underpin the "new world" of computing exemplified by "human–computer symbiosis." It was designed and created in part for educational use, more so for constructionist...
and Pico. The boolean values
are represented as functions of two values that evaluate to one or the other of their arguments.
Formal definition in lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
:
- true ≡
λa.λb. a - false ≡
λa.λb. b
Note that this definition allows predicates (i.e. functions returning logical values) to directly act as if-clauses, e.g. if predicate is a unary predicate,
- predicate x then-clause else-clause
evaluates to then-clause if predicate x evaluates to true, and to else-clause if predicate x evaluates to false.
Functions of boolean arithmetic can be derived for Church booleans:
- and ≡
λm.λn. m n m - or ≡
λm.λn. m m n - not ≡
λm.λa.λb. m b a - xor ≡
λm.λn.λa.λb. m (n b a) (n a b)
Some examples:
- and true false ≡
(λm.λn. m n m) (λa.λb. a) (λa.λb. b) ≡(λa.λb. a) (λa.λb. b) (λa.λb. a)≡(λa.λb. b)≡ false
- or true false ≡
(λm.λn. m m n) (λa.λb. a) (λa.λb. b)≡(λa.λb. a) (λa.λb. a) (λa.λb. b)≡(λa.λb. a)≡ true
- not true ≡
(λm.λa.λb. m b a) (λa.λb. a)≡(λa.λb. (λa.λb. a) b a)≡(λa.λb. b)≡ false
Church pairs
Church pairs are the Church encoding of the pairCons
In computer programming, cons is a fundamental function in most dialects of the Lisp programming language. cons constructs memory objects which hold two values or pointers to values. These objects are referred to as cells, conses, non-atomic s-expressions , or pairs...
(two-tuple) type. The pair is represented as a function that takes a function argument. When given its argument it will apply the argument to the two components of the pair.
Formal definition in lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
:
- pair ≡
λx.λy.λz.z x y - fst ≡
λp.p (λx.λy.x) - snd ≡
λp.p (λx.λy.y)
An example:
- fst (pair a b) ≡
(λp.p (λx.λy.x)) ((λx.λy.λz.z x y) a b) ≡ (λp.p (λx.λy.x)) (λz.z a b) ≡ (λz.z a b) (λx.λy.x) ≡ (λx.λy.x) a b ≡ a
List encodings
An encoding of (immutableImmutable object
In object-oriented and functional programming, an immutable object is an object whose state cannot be modified after it is created. This is in contrast to a mutable object, which can be modified after it is created...
) lists of varying length must define a constructor for creating an empty list (nil), an operation testing whether or not a list is empty (isnil), an operation to prepend a given value to a (possibly empty) list (cons), and two operations to determine the first element and the list of the remaining elements of a nonempty list (head and tail).
Church pairs
A nonempty list can basically be encoded by a Church pair with the head of the list stored in the first component of the pair and the tail of the list in the second component. However, special care is needed to unambiguously encode the empty list. This can be achieved by encapsulating any individual list node within the second component of another pair whose first component contains a Church boolean which is true for the empty list and false otherwise, similar to a tagged unionTagged union
In computer science, a tagged union, also called a variant, variant record, discriminated union, or disjoint union, is a data structure used to hold a value that could take on several different, but fixed types. Only one of the types can be in use at any one time, and a tag field explicitly...
. Using this idea the basic list operations can be defined like this:
- nil ≡ pair true true
- isnil ≡ fst
- cons ≡ λh.λt.pair false (pair h t)
- head ≡ λz.fst (snd z)
- tail ≡ λz.snd (snd z)
The second component of the pair encoding nil is never used provided that head and tail are only applied to nonempty lists.
Alternatively, one can define
- cons ≡ pair
- head ≡ fst
- tail ≡ snd
- nil ≡ false
- isnil ≡ λl.l (λh.λt.λd.false) true
where the last definition is a special case of the general
- process-list ≡ λl.l (λh.λt.λd. head-and-tail-clause) nil-clause
Higher-order function
As an alternative to the encoding using Church pairs, a list can be encoded by identifying it with its right fold functionFold (higher-order function)
In functional programming, fold – also known variously as reduce, accumulate, compress, or inject – are a family of higher-order functions that analyze a recursive data structure and recombine through use of a given combining operation the results of recursively processing its...
. For example, a list of three elements x, y and z can be encoded by a higher-order function which when applied to a combinator c and a value n returns c x (c y (c z n))).
- nil ≡
λc.λn.n - isnil ≡
λl.l (λh.λt.false) true - cons ≡
λh.λt.λc.λn.c h (t c n) - head ≡
λl.l (λh.λt.h) false - tail ≡
λl.fst (l (λx.λp.pair (snd p) (cons x (snd p))) (pair nil nil))
See also
- Lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
- System FSystem FSystem F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
for Church numerals in a typed calculus - Mogensen–Scott encoding