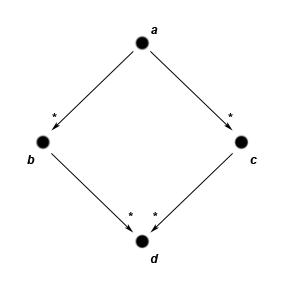
The Church–Rosser theorem states that if there are two distinct reductions starting from the same lambda calculus

Lambda calculus

In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...

 term, then there exists a term that is reachable from each reduct via a (possibly empty) sequence of reductions. This is symbolized by the diagram at right: if term a can be reduced to both b and c, then there must be a further term d (possibly equal to either b or c) to which both b and c can be reduced.

Viewing the lambda calculus as an abstract rewriting system

Abstract rewriting system

In mathematical logic and theoretical computer science, an abstract rewriting system is a formalism that captures the quintessential notion and properties of rewriting systems...

, the Church–Rosser theorem is a theorem of confluence

Confluence (abstract rewriting)

In computer science, confluence is a property of rewriting systems, describing that terms in this system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system.- Motivating example :Consider...

. As a consequence of the theorem, a term in the lambda calculus

Lambda calculus

In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...

 has at most one normal form, justifying reference to "the normal form" of a certain term. The theorem was proved in 1936 by Alonzo Church

Alonzo Church

Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...

 and J. Barkley Rosser.

The Church–Rosser theorem also holds for many variants of the lambda calculus, such as the simply-typed lambda calculus

Simply typed lambda calculus

The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...

, many calculi with advanced type systems, and Gordon Plotkin

Gordon Plotkin

Gordon D. Plotkin, FRS, FRSE is a Scottish computer scientist.Gordon Plotkin is best-known for his introduction of structural operational semantics and his work on denotational semantics. In particular, his notes on A Structural Approach to Operational Semantics of 1981 were very influential...

's beta-value calculus. Plotkin also used a Church–Rosser theorem to prove that the evaluation of functional programs (for both lazy evaluation

Lazy evaluation

In programming language theory, lazy evaluation or call-by-need is an evaluation strategy which delays the evaluation of an expression until the value of this is actually required and which also avoids repeated evaluations...

 and eager evaluation

Eager evaluation

In computer programming, eager evaluation or greedy evaluation is the evaluation strategy in most traditional programming languages. In eager evaluation an expression is evaluated as soon as it gets bound to a variable. The term is typically used to contrast lazy evaluation, where expressions are...

) is a function from programs to values (a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

of the lambda terms).