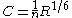Chézy formula
Encyclopedia
In fluid dynamics
, the Chézy formula describes the mean flow velocity
of steady, turbulent
open channel flow
:
where
The formula is named after Antoine de Chézy
, the French hydraulics engineer who devised it in 1775.
where
This relation is empirical.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Chézy formula describes the mean flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
of steady, turbulent
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
open channel flow
Open channel flow
Open-Channel Flow, a branch of Hydraulics, is a type of liquid flow within a conduit with a free surface, known as a channel. The other type of flow within a conduit is pipe flow. These two types of flow are similar in many ways, but differ in one important respect; the free surface...
:
where
is the mean velocity [m/s],
is the Chézy coefficient [m½/s],
is the hydraulic radius (~ water depth) [m], and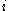
is the bottom slope [m/m].
The formula is named after Antoine de Chézy
Antoine de Chézy
Antoine de Chézy was a French hydraulics engineer. He is known for the Chézy formula, which concerned the velocity of pipe flow. He died in 1798 after being director of the École nationale des ponts et chaussées for less than a year. His son was the orientalist Antoine-Léonard de Chézy.-References:...
, the French hydraulics engineer who devised it in 1775.
Usage with Manning coefficient
This formula can also be used with Manning's Roughness Coefficient, instead of Chézy's coefficient. Manning derived the following relation to C based upon experiments:
where
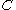is the Chézy coefficient [m½/s],
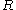is the hydraulic radius (~ water depth) [m], and
is Manning's roughness coefficient.
This relation is empirical.