Circle packing in a circle - AbsoluteAstronomy.com

Circle packing in a circle is a two-dimensional packing problem

Packing problem

Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...

with the objective of packing unit circles into the smallest possible larger circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

.

Minimum solutions:

Number of unit circles	Enclosing circle radius	Density	Optimality
1	1	1.0000	Trivially optimal.
2	2	0.5000	Trivially optimal.
3	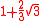≈ 2.154...	0.6466...	Trivially optimal.
4	≈ 2.414...	0.6864...	Trivially optimal.
5	≈ 2.701...	0.6854...	Proved optimal by Graham in 1968.
6	3	0.6667...	Proved optimal by Graham in 1968.
7	3	0.7778...	Proved optimal by Graham in 1968.
8	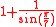≈ 3.304...	0.7328...	Proved optimal by Pirl in 1969.
9	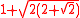≈ 3.613...	0.6895...	Proved optimal by Pirl in 1969.
10	3.813...	0.6878...	Proved optimal by Pirl in 1969.
11	≈ 3.923...	0.7148...	Proved optimal by Melissen in 1994.
12	4.029...	0.7392...	Proved optimal by Fodor in 2000.
13	≈4.236...	0.7245...	Proved optimal by Fodor in 2003.
14	4.328...	0.7474...	Conjectured optimal.
15	4.521...	0.7339...	Conjectured optimal.
16	4.615...	0.7512...	Conjectured optimal.
17	4.792...	0.7403...	Conjectured optimal.
18	≈ 4.863...	0.7611...	Conjectured optimal.
19	≈ 4.863...	0.8034...	Proved optimal by Fodor in 1999.
20	5.122...	0.7623...	Conjectured optimal.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.