
Clairaut's theorem
Encyclopedia
Formula
Clairaut's formula for the acceleration of gravity g on the surface of a spheroid at latitude φ, was:
where G is the value of the acceleration of gravity at the equator, m the ratio of the centrifugal force to gravity at the equator, and f the flattening
Flattening
The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...
of a meridian
Meridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
section of the earth, defined as:
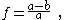
(where a = semimajor axis, b=semiminor axis ).
Clairaut derived the formula under the assumption that the body was composed of concentric coaxial spheroidal layers of constant density.
This work was subsequently pursued by Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, who relaxed the initial assumption that surfaces of equal density were spheroids.
Stokes showed in 1849 that the theorem applied to any law of density so long as the external surface is a spheroid of equilibrium. A history of the subject, and more detailed equations for g can be found in Khan.
The above expression for g has been supplanted by the Somigliana equation:
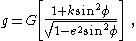
where, for the Earth, G =9.7803267714 ms−2; k =0.00193185138639 ; e2 =0.00669437999013.
Clairaut's relation
A formal mathematical statement of Clairaut's theorem is:Pressley (p. 185) explains this theorem as an expression of conservation of angular momentum about the axis of revolution when a particle slides along a geodesic under no forces other than those that keep it on the surface.
Geodesy
The spheroidal shape of the Earth is the result of the interplay between gravity and centrifugal forceCentrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
caused by the Earth's rotation about its axis. In his Principia, Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
proposed the equilibrium shape of a homogeneous rotating Earth was a rotational ellipsoid with a flattening f given by 1/230. As a result gravity increases from the equator to the poles. By applying Clairaut's theorem, Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
was able to deduce from 15 gravity values that f = 1/330. A modern estimate is 1/298.25642. See Figure of the Earth
Figure of the Earth
The expression figure of the Earth has various meanings in geodesy according to the way it is used and the precision with which the Earth's size and shape is to be defined. The actual topographic surface is most apparent with its variety of land forms and water areas. This is, in fact, the surface...
for more detail.
For a detailed account of the construction of the reference Earth model
Reference ellipsoid
In geodesy, a reference ellipsoid is a mathematically-defined surface that approximates the geoid, the truer figure of the Earth, or other planetary body....
of geodesy, see Chatfield.

