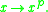Clarkson's inequalities
Encyclopedia
In mathematics
, Clarkson's inequalities are results in the theory of Lp spaces
. They give bounds for the Lp-norm
s of the sum and difference of two measurable function
s in Lp in terms of the Lp-norms of those functions individually.
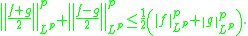
For 1 < p < 2,
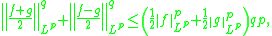
where
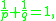
i.e., q = p ⁄ (p − 1).
The case p ≥ 2 is somewhat easier to prove, being a simple application of the triangle inequality
and the convexity
of
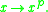
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Clarkson's inequalities are results in the theory of Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. They give bounds for the Lp-norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
s of the sum and difference of two measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s in Lp in terms of the Lp-norms of those functions individually.
Statement of the inequalities
Let (X, Σ, μ) be a measure space; let f, g : X → R be measurable functions in Lp. Then, for 2 ≤ p < +∞,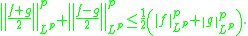
For 1 < p < 2,
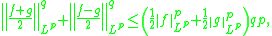
where
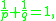
i.e., q = p ⁄ (p − 1).
The case p ≥ 2 is somewhat easier to prove, being a simple application of the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
and the convexity
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
of