
Clebsch surface
Encyclopedia
In mathematics, the Clebsch diagonal cubic surface, or Klein's icosahedral cubic surface is a cubic surface
studied by and all of whose 27 exceptional lines
can be defined over the real numbers. The term Klein's icosahedral surface can refer to either this surface or its blowup at the 10 Eckardt points.


Eliminating x0 shows that it is also isomorphic to the surface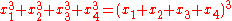
in P3.
The symmetry group of the surface is the symmetric group
S5 of order 120, acting by permutations of the coordinates (in P4). Up to isomorphism, the Clebsch surface is the only cubic surface with this automorphism group.
The surface has 10 Eckardt points where 3 lines meet, given by the point
(1 : −1 : 0 : 0 : 0) and its conjugates under permutations. showed that the surface obtained by blowing up the Clebsch surface in its 10 Eckardt points is the Hilbert modular surface
of the level 2 principal congruence subgroup of the Hilbert modular group of the field Q(√5). The quotient of the Hilbert modular group by its level 2 congruence subgroup is isomorphic to the alternating group of order 60 on 5 points.
Like all nonsingular cubic surfaces, the Clebsch cubic can be obtained by blowing up the projective plane in 6 points. described these points as follows. If the projective plane is identified with the set of lines through the origin in a 3-dimensional vector space containing an icosahedron centered at the origin, then the 6 points correspond to the 6 lines through the centers of the 12 vertices. The Eckardt points correspond to the 10 lines through the centers of the 20 faces.
Cubic surface
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single polynomial which is homogeneous of degree 3...
studied by and all of whose 27 exceptional lines
can be defined over the real numbers. The term Klein's icosahedral surface can refer to either this surface or its blowup at the 10 Eckardt points.
Definition
The Clebsch surface is the set of points (x0:x1:x2:x3:x4) of P4 satisfying the equations

Eliminating x0 shows that it is also isomorphic to the surface
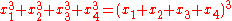
in P3.
The symmetry group of the surface is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S5 of order 120, acting by permutations of the coordinates (in P4). Up to isomorphism, the Clebsch surface is the only cubic surface with this automorphism group.
Properties
The 27 exceptional lines are:- The 15 images (under S5) of the line of points of the form (a : −a : b : −b : 0).
- The 12 images of the line though the point (1:ζ: ζ2: ζ3: ζ4) and its complex conjugate, where ζ is a primitive 5th root of 1.
The surface has 10 Eckardt points where 3 lines meet, given by the point
(1 : −1 : 0 : 0 : 0) and its conjugates under permutations. showed that the surface obtained by blowing up the Clebsch surface in its 10 Eckardt points is the Hilbert modular surface
Hilbert modular surface
In mathematics, a Hilbert modular surface is one of the surfaces obtained by taking a quotient of a product of two copies of the upper half-plane by a Hilbert modular group....
of the level 2 principal congruence subgroup of the Hilbert modular group of the field Q(√5). The quotient of the Hilbert modular group by its level 2 congruence subgroup is isomorphic to the alternating group of order 60 on 5 points.
Like all nonsingular cubic surfaces, the Clebsch cubic can be obtained by blowing up the projective plane in 6 points. described these points as follows. If the projective plane is identified with the set of lines through the origin in a 3-dimensional vector space containing an icosahedron centered at the origin, then the 6 points correspond to the 6 lines through the centers of the 12 vertices. The Eckardt points correspond to the 10 lines through the centers of the 20 faces.

