
Clenshaw algorithm
Encyclopedia
In numerical analysis
, the Clenshaw algorithm is a recursive
method to evaluate a linear combination of Chebyshev polynomials
. In general it applies to any class of functions that can be defined by a three-term recurrence relation
.
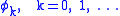 is a sequence of functions that satisfy the linear recurrence relation
is a sequence of functions that satisfy the linear recurrence relation
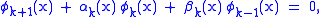
where the coefficients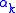 and
and 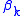 are known in advance. For any finite sequence
are known in advance. For any finite sequence  , define the functions
, define the functions 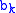 by the "reverse" recurrence formula:
by the "reverse" recurrence formula:
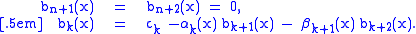
The linear combination of the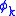 satisfies:
satisfies:
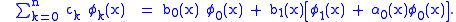
See Fox and Parker for more information and stability analyses.
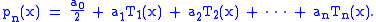
The coefficients in the recursion relation for the Chebyshev polynomials
are
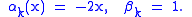
Therefore, using the identities
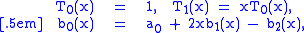
Clenshaw's algorithm reduces to:
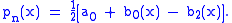
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the Clenshaw algorithm is a recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
method to evaluate a linear combination of Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
. In general it applies to any class of functions that can be defined by a three-term recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
.
Clenshaw algorithm
Suppose that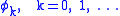 is a sequence of functions that satisfy the linear recurrence relation
is a sequence of functions that satisfy the linear recurrence relation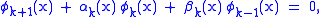
where the coefficients
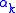 and
and 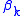 are known in advance. For any finite sequence
are known in advance. For any finite sequence  , define the functions
, define the functions 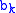 by the "reverse" recurrence formula:
by the "reverse" recurrence formula: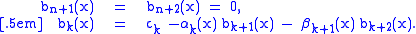
The linear combination of the
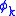 satisfies:
satisfies: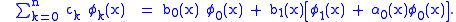
See Fox and Parker for more information and stability analyses.
Special case for Chebyshev series
Consider a truncated Chebyshev series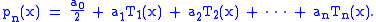
The coefficients in the recursion relation for the Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
are
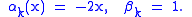
Therefore, using the identities
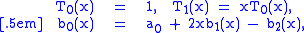
Clenshaw's algorithm reduces to:
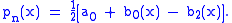
See also
- Horner schemeHorner schemeIn numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
to evaluate polynomials in monomial form - De Casteljau's algorithmDe Casteljau's algorithmIn the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau...
to evaluate polynomials in Bézier form

