Closest pair of points problem
Encyclopedia
The closest pair of points problem or closest pair problem is a problem of computational geometry
: given n points in metric space
, find a pair of points with the smallest distance between them. Its two-dimensional version, for points in the Euclidean plane, was among the first geometric problems which were treated at the origins of the systematic study of the computational complexity
of geometric algorithms.
A naive algorithm of finding distances between all pairs of points and selecting the minimum requires O(dn2) time. It turns out that the problem may be solved in O(n log n) time in an Euclidean space
or Lp space
of fixed dimension d. In the algebraic decision tree model of computation
, the O(n log n) algorithm is optimal. The optimality follows from the observation that the element uniqueness problem
(with the lower bound of Ω(n log n) for time complexity) is reducible to the closest pair problem: checking whether the minimal distance is 0 after the solving of the closest pair problem answers the question whether there are two coinciding points.
In the computational model which assumes that the floor function
is computable in constant time the problem can be solved in O(n log log n) time. If we allow randomization to be used together with the floor function, the problem can be solved in O(n) time.
(n2) time
. To do that, one could compute the distances between all the pairs of points, then pick the pair with the smallest distance, as illustrated below.
minDist = infinity
for each p in P:
for each q in P:
if p ≠ q and dist(p, q) < minDist:
minDist = dist(p, q)
closestPair = (p, q)
return closestPair
divide and conquer approach, e.g., as follows:
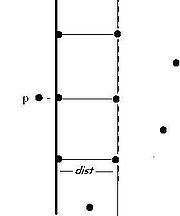It turns out that step 4 may be accomplished in linear time. Again, a naive approach would require the calculation of distances for all left-right pairs, i.e., in quadratic time. The key observation is based on the following sparsity property of the point set. We already know that the closest pair of points is no further apart than 
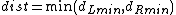. Therefore for each point 
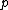of the left of the dividing line we have to compare the distances to the points that lie in the rectangle of dimensions (dist, 2 * dist) to the right of the dividing line, as shown in the figure. And what is more, this rectangle can contain at most 6 points with pairwise distances at most 
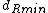. Therefore it is sufficient to compute at most 8(n) left-right distances in step 4. The recurrence relation for the number of steps can be written as 
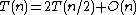, which we can solve using the master theorem
to get O(n log n).
As the closest pair of points define an edge in the Delaunay triangulation
, and correspond to two adjacent cells in the Voronoi diagram
, the closest pair of points can be determined in linear time when we are given one of these two structures. Computing either the Delaunay triangulation or the Voronoi diagram takes O(n log n) time. These approaches are not efficient for dimension d>2, while the divide and conquer algorithm can be generalized to take O(n log n) time for any constant value of d.
for the closest-pair problem is stated as follows:
If the bounding box for all points is known in advance and the constant-time floor function is available, then the expected O(n) space data structure was suggested that supports expected-time O(log n) insertions and deletions and constant query time. When modified for the algebraic decision tree model, insertions and deletions would require O(log2 n) expected time. It is worth noting, though, that the complexity of the dynamic closest pair algorithm cited above is exponential in the dimension d, and therefore such an algorithm becomes less suitable for high-dimensional problems.
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
: given n points in metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, find a pair of points with the smallest distance between them. Its two-dimensional version, for points in the Euclidean plane, was among the first geometric problems which were treated at the origins of the systematic study of the computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of geometric algorithms.
A naive algorithm of finding distances between all pairs of points and selecting the minimum requires O(dn2) time. It turns out that the problem may be solved in O(n log n) time in an Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
or Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
of fixed dimension d. In the algebraic decision tree model of computation
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...
, the O(n log n) algorithm is optimal. The optimality follows from the observation that the element uniqueness problem
Element uniqueness problem
In computational complexity theory, the element distinctness problem or element uniqueness problem is the problem of determining whether all the elements of a list are distinct.It is a well studied problem in many different models of computation...
(with the lower bound of Ω(n log n) for time complexity) is reducible to the closest pair problem: checking whether the minimal distance is 0 after the solving of the closest pair problem answers the question whether there are two coinciding points.
In the computational model which assumes that the floor function
Floor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
is computable in constant time the problem can be solved in O(n log log n) time. If we allow randomization to be used together with the floor function, the problem can be solved in O(n) time.
Brute-force algorithm
The closest pair of points can easily be computed in OBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n2) time
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
. To do that, one could compute the distances between all the pairs of points, then pick the pair with the smallest distance, as illustrated below.
minDist = infinity
for each p in P:
for each q in P:
if p ≠ q and dist(p, q) < minDist:
minDist = dist(p, q)
closestPair = (p, q)
return closestPair
Planar case
The problem can be solved in O(n log n) time using the recursiveRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
divide and conquer approach, e.g., as follows:
- Sort points along the x-coordinate
- Split the set of points into two equal-sized subsets by a vertical line
- Solve the problem recursively in the left and right subsets. This will give the left-side and right-side minimal distances
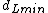and 
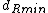respectively. - Find the minimal distance
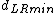among the pair of points in which one point lies on the left of the dividing vertical and the second point lies to the right. - The final answer is the minimum among
, 
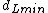, and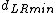 
.
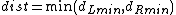. Therefore for each point 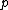of the left of the dividing line we have to compare the distances to the points that lie in the rectangle of dimensions (dist, 2 * dist) to the right of the dividing line, as shown in the figure. And what is more, this rectangle can contain at most 6 points with pairwise distances at most 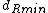. Therefore it is sufficient to compute at most 8(n) left-right distances in step 4. The recurrence relation for the number of steps can be written as 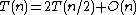, which we can solve using the master theoremMaster theorem
In the analysis of algorithms, the master theorem provides a cookbook solution in asymptotic terms for recurrence relations of types that occur in the analysis of many divide and conquer algorithms...
to get O(n log n).
As the closest pair of points define an edge in the Delaunay triangulation
Delaunay triangulation
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
, and correspond to two adjacent cells in the Voronoi diagram
Voronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
, the closest pair of points can be determined in linear time when we are given one of these two structures. Computing either the Delaunay triangulation or the Voronoi diagram takes O(n log n) time. These approaches are not efficient for dimension d>2, while the divide and conquer algorithm can be generalized to take O(n log n) time for any constant value of d.
Dynamic closest-pair problem
The dynamic versionDynamic problem (algorithms)
Dynamic problems in computational complexity theory are problems stated in terms of the changing input data. In the most general form a problem in this category is usually stated as follows:...
for the closest-pair problem is stated as follows:
- Given a dynamic set of objects, find algorithms and data structureData structureIn computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s for efficient recalculation of the closest pair of objects each time the objects are inserted or deleted.
If the bounding box for all points is known in advance and the constant-time floor function is available, then the expected O(n) space data structure was suggested that supports expected-time O(log n) insertions and deletions and constant query time. When modified for the algebraic decision tree model, insertions and deletions would require O(log2 n) expected time. It is worth noting, though, that the complexity of the dynamic closest pair algorithm cited above is exponential in the dimension d, and therefore such an algorithm becomes less suitable for high-dimensional problems.