Co-occurrence matrix
Encyclopedia
A co-occurrence matrix or co-occurrence distribution (less often coöccurrence matrix or coöccurrence distribution) is a matrix
or distribution
that is defined over an image
to be the distribution of co-occurring values at a given offset. Mathematically, a co-occurrence matrix C is defined over an n x m image I, parameterized by an offset (Δx,Δy), as:
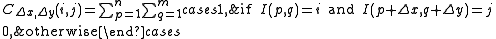
The 'value' of the image originally referred to the grayscale
value of the specified pixel
. The value could be anything, from a binary
on/off value to 32-bit color and beyond. Note that 32-bit color will yield a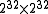
co-occurrence matrix!
Really any matrix or pair of matrices can be used to generate a co-occurrence matrix, though their main applicability has been in the measuring of texture in images, so the typical definition, as above, assumes that the matrix is in fact an image.
It is also possible to define the matrix across two different images. Such a matrix can then be used for color mapping
.
Note that the (Δx,Δy) parameterization makes the co-occurrence matrix sensitive to rotation. We choose one offset vector, so a rotation of the image not equal to 180 degrees will result in a different co-occurrence distribution for the same (rotated) image. This is rarely desirable in the applications co-occurrence matrices are used in, so the co-occurrence matrix is often formed using a set of offsets sweeping through 180 degrees (i.e. 0, 45, 90, and 135 degrees) at the same distance to achieve a degree of rotational invariance
.
values of the image or various dimensions of color, the co-occurrence matrix can measure the texture of the image. Because co-occurrence matrices are typically large and sparse, various metrics of the matrix are often taken to get a more useful set of features. Features generated using this technique are usually called Haralick features, after R M Haralick, attributed to his paper Textural features for image classification (1973).
Texture measures like the co-occurrence matrix, wavelet transforms, and model fitting have found application in medical image analysis in particular.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
or distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
that is defined over an image
Digital image
A digital image is a numeric representation of a two-dimensional image. Depending on whether or not the image resolution is fixed, it may be of vector or raster type...
to be the distribution of co-occurring values at a given offset. Mathematically, a co-occurrence matrix C is defined over an n x m image I, parameterized by an offset (Δx,Δy), as:
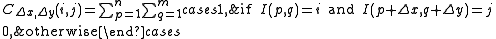
The 'value' of the image originally referred to the grayscale
Grayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
value of the specified pixel
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
. The value could be anything, from a binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
on/off value to 32-bit color and beyond. Note that 32-bit color will yield a
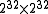co-occurrence matrix!Really any matrix or pair of matrices can be used to generate a co-occurrence matrix, though their main applicability has been in the measuring of texture in images, so the typical definition, as above, assumes that the matrix is in fact an image.
It is also possible to define the matrix across two different images. Such a matrix can then be used for color mapping
Color mapping
Color mapping is a function that maps the colors of one image to the colors of another image. A color mapping may be referred to as the algorithm that results in the mapping function or the algorithm that transforms the image colors...
.
Note that the (Δx,Δy) parameterization makes the co-occurrence matrix sensitive to rotation. We choose one offset vector, so a rotation of the image not equal to 180 degrees will result in a different co-occurrence distribution for the same (rotated) image. This is rarely desirable in the applications co-occurrence matrices are used in, so the co-occurrence matrix is often formed using a set of offsets sweeping through 180 degrees (i.e. 0, 45, 90, and 135 degrees) at the same distance to achieve a degree of rotational invariance
Rotational invariance
In mathematics, a function defined on an inner product space is said to have rotational invariance if its value does not change when arbitrary rotations are applied to its argument...
.
Aliases
Co-occurrence matrices have been referred to as:- GLCM (Gray-Level Co-occurrence Matrices)
- spatial dependence matrix
Application to image analysis
Whether considering the intensity or grayscaleGrayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
values of the image or various dimensions of color, the co-occurrence matrix can measure the texture of the image. Because co-occurrence matrices are typically large and sparse, various metrics of the matrix are often taken to get a more useful set of features. Features generated using this technique are usually called Haralick features, after R M Haralick, attributed to his paper Textural features for image classification (1973).
Texture measures like the co-occurrence matrix, wavelet transforms, and model fitting have found application in medical image analysis in particular.