
Complete sequence
Encyclopedia
In mathematics
, an integer sequence
is called a complete sequence if every positive integer can be expressed as a sum of values in the sequence, using each value at most once.
For example, the sequence of powers of two {1, 2, 4, 8, ...}, based on the binary numeral system
, is a complete sequence; given any natural number, we can choose the values corresponding to the 1 bits in its binary representation and sum them to obtain that number (e.g. 37 = 1001012 = 1 + 4 + 32). This sequence is minimal, since no value can be removed from it without making some natural numbers impossible to represent. Simple examples of sequences that are not complete include:
Without loss of generality, assume the sequence an is in nondecreasing order, and define the partial sums of an as:
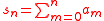 .
.
Then the conditions
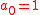

are both necessary and sufficient for an to be a complete sequence.
Other complete sequences include:
For example, in the Fibonacci arithmetic system, based on the Fibonacci sequence, the number 17 can be encoded in six different ways:
In this numeral system, any substring "100" can be replaced by "011" and vice versa due to the definition of the Fibonacci numbers.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
is called a complete sequence if every positive integer can be expressed as a sum of values in the sequence, using each value at most once.
For example, the sequence of powers of two {1, 2, 4, 8, ...}, based on the binary numeral system
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
, is a complete sequence; given any natural number, we can choose the values corresponding to the 1 bits in its binary representation and sum them to obtain that number (e.g. 37 = 1001012 = 1 + 4 + 32). This sequence is minimal, since no value can be removed from it without making some natural numbers impossible to represent. Simple examples of sequences that are not complete include:
- The even numbers; since adding even numbers produces only even numbers, no odd number can be formed.
- Powers of three; no integer having a digit "2" in its ternary representation (2, 5, 6...) can be formed.
Without loss of generality, assume the sequence an is in nondecreasing order, and define the partial sums of an as:
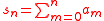 .
.Then the conditions
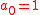

are both necessary and sufficient for an to be a complete sequence.
Other complete sequences include:
- The sequence of the number 1 followed by the prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s; this follows from Bertrand's postulate. - The Fibonacci numbers, as well as the Fibonacci numbers with any one number removed. This follows from the identity that the sum of the first n Fibonacci numbers is the (n + 2)nd Fibonacci number minus 1 (see Fibonacci numbers#Second identity).
Applications
Just as the powers of two form a complete sequence due to the binary numeral system, in fact any complete sequence can be used to encode integers as bit strings. The rightmost bit position is assigned to the first, smallest member of the sequence; the next rightmost to the next member; and so on. Bits set to 1 are included in the sum. These representations may not be unique.For example, in the Fibonacci arithmetic system, based on the Fibonacci sequence, the number 17 can be encoded in six different ways:
- 110111 (F6 + F5 + F3 + F2 + F1 = 8 + 5 + 2 + 1 + 1 = 17, maximal form)
- 111001 (F6 + F5 + F4 + F1 = 8 + 5 + 3 + 1 = 17)
- 111010 (F6 + F5 + F4 + F2 = 8 + 5 + 3 + 1 = 17)
- 1000111 (F7 + F3 + F2 + F1 = 13 + 2 + 1 + 1 = 17)
- 1001001 (F7 + F4 + F1 = 13 + 3 + 1 = 17)
- 1001010 (F7 + F4 + F2 = 13 + 3 + 1 = 17, minimal form, as used in Fibonacci codingFibonacci codingIn mathematics, Fibonacci coding is a universal code which encodes positive integers into binary code words. Each code word ends with "11" and contains no other instances of "11" before the end.-Definition:...
)
In this numeral system, any substring "100" can be replaced by "011" and vice versa due to the definition of the Fibonacci numbers.

