Complex network zeta function
Encyclopedia
Different definitions have been given for the dimension of a complex network
or graph
. For example, metric dimension
is defined in terms of the resolving set for a graph. Dimension has also been defined
based on the box covering method
applied to graphs. Here we describe the definition based on the complex network zeta function. This generalises the definition based on the scaling property of the volume with distance. The best definition depends on the application.
We denote by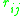 the distance from node
the distance from node  to node
to node  , i.e., the length of the shortest path connecting the first node to the second node.
, i.e., the length of the shortest path connecting the first node to the second node. 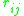 is
is  if there is no path from node
if there is no path from node  to node
to node 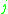 . With this definition, the nodes of the complex network become points in a metric space
. With this definition, the nodes of the complex network become points in a metric space
. Simple generalisations of this definition can be studied, e.g., we could consider weighted edges. The graph surface function,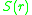 , is defined as the number of nodes which are exactly at a distance
, is defined as the number of nodes which are exactly at a distance  from a given node, averaged over all nodes of the network. The complex network zeta function
from a given node, averaged over all nodes of the network. The complex network zeta function 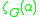 is defined as
is defined as
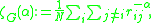
where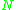 is the graph size, measured by the number of nodes. When
is the graph size, measured by the number of nodes. When  is zero all nodes contribute equally to the sum in the previous equation. This means that
is zero all nodes contribute equally to the sum in the previous equation. This means that 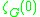 is
is  , and it diverges when
, and it diverges when  . When the exponent
. When the exponent  tends to infinity, the sum gets contributions only from the nearest neighbours of a node. The other terms tend to zero. Thus,
tends to infinity, the sum gets contributions only from the nearest neighbours of a node. The other terms tend to zero. Thus,  tends to the average degree
tends to the average degree  for the graph as
for the graph as 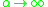 .
.
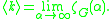
The need for taking an average over all nodes can be avoided by using the concept of supremum over nodes, which makes the concept much easier to apply for formally infinite graphs.The definition can be expressed as a weighted sum over the node distances. This gives the Dirichlet series relation

This definition has been used in the shortcut model
to study several processes and their dependence on dimension.
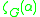 is a decreasing function of
is a decreasing function of  ,
, 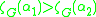 , if
, if  . If the average degree of the nodes (the mean coordination number for the graph) is finite, then there is exactly one value of
. If the average degree of the nodes (the mean coordination number for the graph) is finite, then there is exactly one value of  ,
, 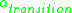 , at which the complex network zeta function transitions from being infinite to being finite. This has been defined as the dimension of the complex network. If we add more edges to an existing graph, the distances between nodes will decrease. This results in an increase in the value of the complex network zeta function, since
, at which the complex network zeta function transitions from being infinite to being finite. This has been defined as the dimension of the complex network. If we add more edges to an existing graph, the distances between nodes will decrease. This results in an increase in the value of the complex network zeta function, since  will get pulled inward. If the new links connect remote parts of the system, i.e., if the distances change by amounts which do not remain finite as the graph size
will get pulled inward. If the new links connect remote parts of the system, i.e., if the distances change by amounts which do not remain finite as the graph size  , then the dimension tends to increase. For regular discrete d-dimensional lattices
, then the dimension tends to increase. For regular discrete d-dimensional lattices  with distance defined using the
with distance defined using the 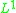 norm
norm
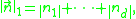
the transition occurs at . The definition of dimension using the complex network zeta function satisfies properties like monotonicity (a subset has a lower or the same dimension as its containing set), stability (a union of sets has the maximum dimension of the component sets forming the union) and Lipschitz invariance , provided the operations involved change the distances between nodes only by finite amounts as the graph size
. The definition of dimension using the complex network zeta function satisfies properties like monotonicity (a subset has a lower or the same dimension as its containing set), stability (a union of sets has the maximum dimension of the component sets forming the union) and Lipschitz invariance , provided the operations involved change the distances between nodes only by finite amounts as the graph size 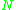 goes to
goes to  . Algorithms to calculate the complex network zeta function have been presented.
. Algorithms to calculate the complex network zeta function have been presented.
 is exactly two for all values of
is exactly two for all values of  (there are two nearest neighbours, two next-nearest neighbours, and so on). Thus, the complex network zeta function
(there are two nearest neighbours, two next-nearest neighbours, and so on). Thus, the complex network zeta function 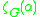 is equal to
is equal to  , where
, where 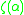 is the usual Riemann zeta function. By choosing a given axis of the lattice and summing over cross-sections for the allowed range of distances along the chosen axis the recursion relation below can be derived
is the usual Riemann zeta function. By choosing a given axis of the lattice and summing over cross-sections for the allowed range of distances along the chosen axis the recursion relation below can be derived

From combinatorics the surface function for a regular lattice can be written as
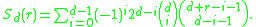
The following expression for the sum of positive integers raised to a given power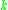 will be useful to calculate the surface function for higher values of
will be useful to calculate the surface function for higher values of 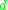 :
:
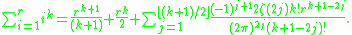
Another formula for the sum of positive integers raised to a given power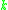 is
is

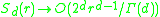 as
as  .
.
The Complex network zeta function for some lattices is given below.
 :
: 
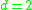 :
: 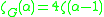
 :
:  )
)
 :
: 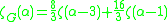
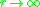 :
:  (for
(for  near the transition point.)
near the transition point.)
 of vertices, in which each pair is connected with probability
of vertices, in which each pair is connected with probability 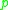 , or else the pair is disconnected. Random graphs have a diameter of two with probability approaching one, in the infinite limit (
, or else the pair is disconnected. Random graphs have a diameter of two with probability approaching one, in the infinite limit ( ). To see this, consider two nodes
). To see this, consider two nodes 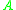 and
and  . For any node
. For any node 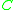 different from
different from  or
or 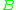 , the probability that
, the probability that  is not simultaneously connected to both
is not simultaneously connected to both  and
and 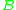 is
is 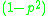 . Thus, the probability that none of the
. Thus, the probability that none of the 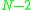 nodes provides a path of length
nodes provides a path of length 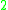 between nodes
between nodes 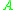 and
and 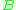 is
is  . This goes to zero as the system size goes to infinity, and hence most random graphs have their nodes connected by paths of length at most
. This goes to zero as the system size goes to infinity, and hence most random graphs have their nodes connected by paths of length at most  . Also, the mean vertex degree will be
. Also, the mean vertex degree will be  . For large random graphs almost all nodes are at a distance of one or two from any given node,
. For large random graphs almost all nodes are at a distance of one or two from any given node, 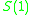 is
is 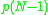 ,
, 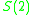 is
is 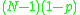 , and the graph zeta function is
, and the graph zeta function is
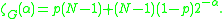
Complex network
In the context of network theory, a complex network is a graph with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in real graphs...
or graph
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. For example, metric dimension
Metric dimension (graph theory)
In graph theory, the metric dimension of a graph G is the minimum number of vertices in a subset S of G such that all other vertices are uniquely determined by their distances to the vertices in S...
is defined in terms of the resolving set for a graph. Dimension has also been defined
Fractal dimension on networks
-Self-similarity of complex networks:Many real networks have two fundamental properties, scale-free property and small-world property. If the degree distribution of the network follows a power-law, the network is scale-free; if any two arbitrary nodes in a network can be connected in a very small...
based on the box covering method
Minkowski-Bouligand dimension
thumb|450px|Estimating the box-counting dimension of the coast of Great BritainIn fractal geometry, the Minkowski–Bouligand dimension, also known as Minkowski dimension or box-counting dimension, is a way of determining the fractal dimension of a set S in a Euclidean space Rn, or more generally in...
applied to graphs. Here we describe the definition based on the complex network zeta function. This generalises the definition based on the scaling property of the volume with distance. The best definition depends on the application.
Definition
One usually thinks of dimension for a set which is dense, like the points on a line, for example. Dimension makes sense in a discrete setting, like for graphs, only in the large system limit, as the size tends to infinity. For example, in Statistical Mechanics, one considers discrete points which are located on regular lattices of different dimensions. Such studies have been extended to arbitrary networks, and it is interesting to consider how the definition of dimension can be extended to cover these cases. A very simple and obvious way to extend the definition of dimension to arbitrary large networks is to consider how the volume (number of nodes within a given distance from a specified node) scales as the distance (shortest path connecting two nodes in the graph) is increased. For many systems arising in physics, this is indeed a useful approach. This definition of dimension could be put on a strong mathematical foundation, similar to the definition of Hausdorff dimension for continuous systems. The mathematically robust definition uses the concept of a zeta function for a graph. The complex network zeta function and the graph surface function were introduced to characterize large graphs. They have also been applied to study patterns in Language Analysis. In this section we will briefly review the definition of the functions and discuss further some of their properties which follow from the definition.We denote by
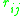 the distance from node
the distance from node  to node
to node  , i.e., the length of the shortest path connecting the first node to the second node.
, i.e., the length of the shortest path connecting the first node to the second node. 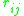 is
is  if there is no path from node
if there is no path from node  to node
to node 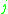 . With this definition, the nodes of the complex network become points in a metric space
. With this definition, the nodes of the complex network become points in a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. Simple generalisations of this definition can be studied, e.g., we could consider weighted edges. The graph surface function,
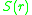 , is defined as the number of nodes which are exactly at a distance
, is defined as the number of nodes which are exactly at a distance  from a given node, averaged over all nodes of the network. The complex network zeta function
from a given node, averaged over all nodes of the network. The complex network zeta function 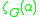 is defined as
is defined as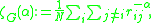
where
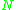 is the graph size, measured by the number of nodes. When
is the graph size, measured by the number of nodes. When  is zero all nodes contribute equally to the sum in the previous equation. This means that
is zero all nodes contribute equally to the sum in the previous equation. This means that 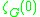 is
is  , and it diverges when
, and it diverges when  . When the exponent
. When the exponent  tends to infinity, the sum gets contributions only from the nearest neighbours of a node. The other terms tend to zero. Thus,
tends to infinity, the sum gets contributions only from the nearest neighbours of a node. The other terms tend to zero. Thus,  tends to the average degree
tends to the average degree  for the graph as
for the graph as 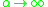 .
.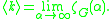
The need for taking an average over all nodes can be avoided by using the concept of supremum over nodes, which makes the concept much easier to apply for formally infinite graphs.The definition can be expressed as a weighted sum over the node distances. This gives the Dirichlet series relation

This definition has been used in the shortcut model
Shortcut model
An important question in statistical mechanics is the dependence of model behaviour on the dimension of the system. The shortcut model was introduced in the course of studying this dependence. The model interpolates between discrete regular lattices of integer dimension.-Introduction:The behaviour...
to study several processes and their dependence on dimension.
Properties
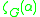 is a decreasing function of
is a decreasing function of  ,
, 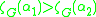 , if
, if  . If the average degree of the nodes (the mean coordination number for the graph) is finite, then there is exactly one value of
. If the average degree of the nodes (the mean coordination number for the graph) is finite, then there is exactly one value of  ,
, 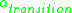 , at which the complex network zeta function transitions from being infinite to being finite. This has been defined as the dimension of the complex network. If we add more edges to an existing graph, the distances between nodes will decrease. This results in an increase in the value of the complex network zeta function, since
, at which the complex network zeta function transitions from being infinite to being finite. This has been defined as the dimension of the complex network. If we add more edges to an existing graph, the distances between nodes will decrease. This results in an increase in the value of the complex network zeta function, since  will get pulled inward. If the new links connect remote parts of the system, i.e., if the distances change by amounts which do not remain finite as the graph size
will get pulled inward. If the new links connect remote parts of the system, i.e., if the distances change by amounts which do not remain finite as the graph size  , then the dimension tends to increase. For regular discrete d-dimensional lattices
, then the dimension tends to increase. For regular discrete d-dimensional lattices  with distance defined using the
with distance defined using the 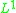 norm
norm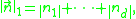
the transition occurs at
 . The definition of dimension using the complex network zeta function satisfies properties like monotonicity (a subset has a lower or the same dimension as its containing set), stability (a union of sets has the maximum dimension of the component sets forming the union) and Lipschitz invariance , provided the operations involved change the distances between nodes only by finite amounts as the graph size
. The definition of dimension using the complex network zeta function satisfies properties like monotonicity (a subset has a lower or the same dimension as its containing set), stability (a union of sets has the maximum dimension of the component sets forming the union) and Lipschitz invariance , provided the operations involved change the distances between nodes only by finite amounts as the graph size 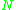 goes to
goes to  . Algorithms to calculate the complex network zeta function have been presented.
. Algorithms to calculate the complex network zeta function have been presented.Values for discrete regular lattices
For a one-dimensional regular lattice the graph surface function is exactly two for all values of
is exactly two for all values of  (there are two nearest neighbours, two next-nearest neighbours, and so on). Thus, the complex network zeta function
(there are two nearest neighbours, two next-nearest neighbours, and so on). Thus, the complex network zeta function 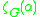 is equal to
is equal to  , where
, where 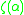 is the usual Riemann zeta function. By choosing a given axis of the lattice and summing over cross-sections for the allowed range of distances along the chosen axis the recursion relation below can be derived
is the usual Riemann zeta function. By choosing a given axis of the lattice and summing over cross-sections for the allowed range of distances along the chosen axis the recursion relation below can be derived
From combinatorics the surface function for a regular lattice can be written as
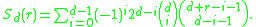
The following expression for the sum of positive integers raised to a given power
 will be useful to calculate the surface function for higher values of
will be useful to calculate the surface function for higher values of 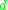 :
: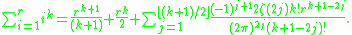
Another formula for the sum of positive integers raised to a given power
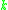 is
is
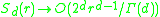 as
as  .
.The Complex network zeta function for some lattices is given below.
 :
: 
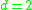 :
: 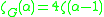
 :
:  )
) :
: 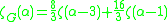
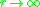 :
:  (for
(for  near the transition point.)
near the transition point.)Random graph zeta function
Random graphs are networks having some number of vertices, in which each pair is connected with probability
of vertices, in which each pair is connected with probability 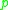 , or else the pair is disconnected. Random graphs have a diameter of two with probability approaching one, in the infinite limit (
, or else the pair is disconnected. Random graphs have a diameter of two with probability approaching one, in the infinite limit ( ). To see this, consider two nodes
). To see this, consider two nodes 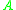 and
and  . For any node
. For any node 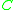 different from
different from  or
or 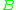 , the probability that
, the probability that  is not simultaneously connected to both
is not simultaneously connected to both  and
and 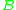 is
is 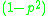 . Thus, the probability that none of the
. Thus, the probability that none of the 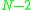 nodes provides a path of length
nodes provides a path of length 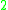 between nodes
between nodes 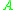 and
and 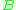 is
is  . This goes to zero as the system size goes to infinity, and hence most random graphs have their nodes connected by paths of length at most
. This goes to zero as the system size goes to infinity, and hence most random graphs have their nodes connected by paths of length at most  . Also, the mean vertex degree will be
. Also, the mean vertex degree will be  . For large random graphs almost all nodes are at a distance of one or two from any given node,
. For large random graphs almost all nodes are at a distance of one or two from any given node, 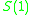 is
is 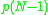 ,
, 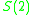 is
is 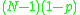 , and the graph zeta function is
, and the graph zeta function is